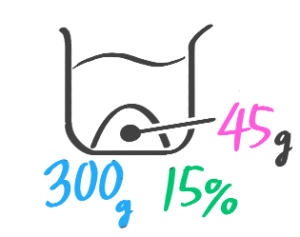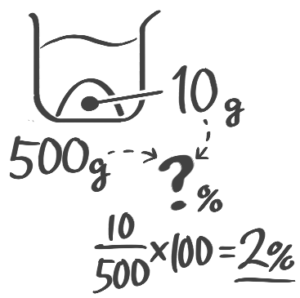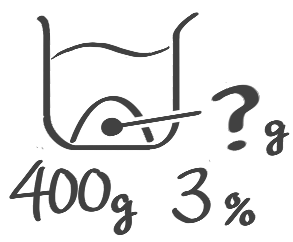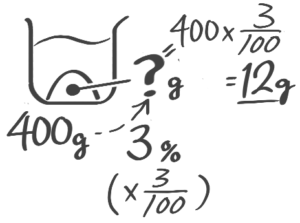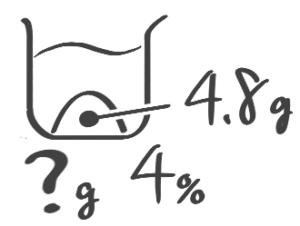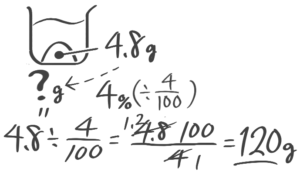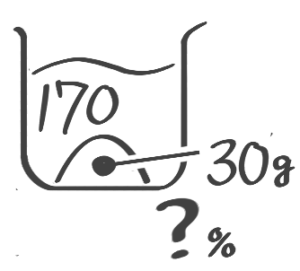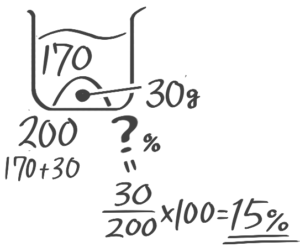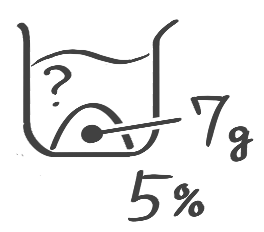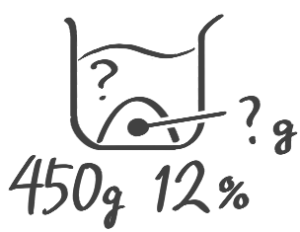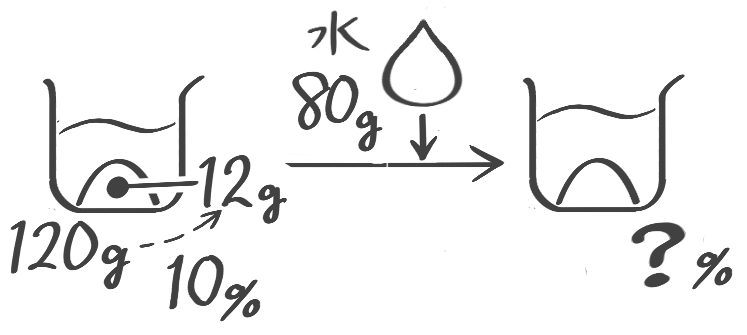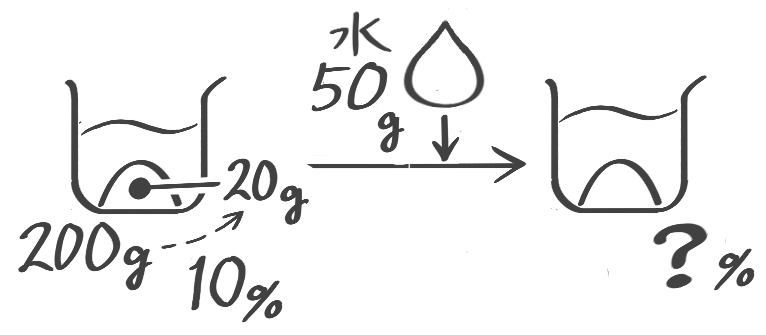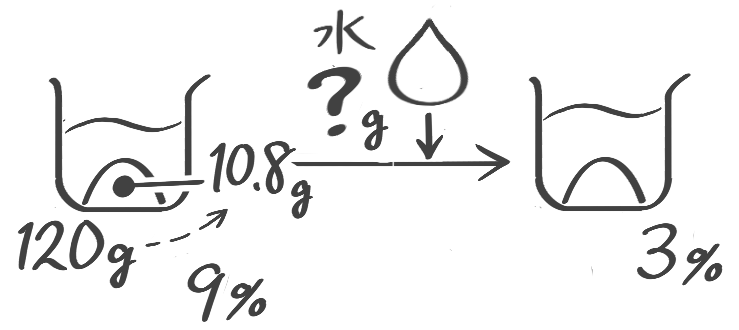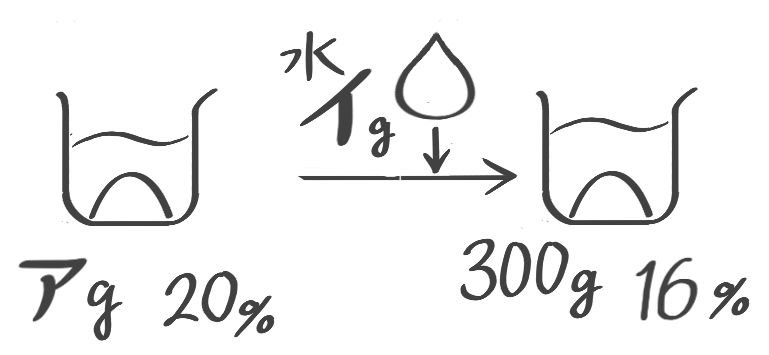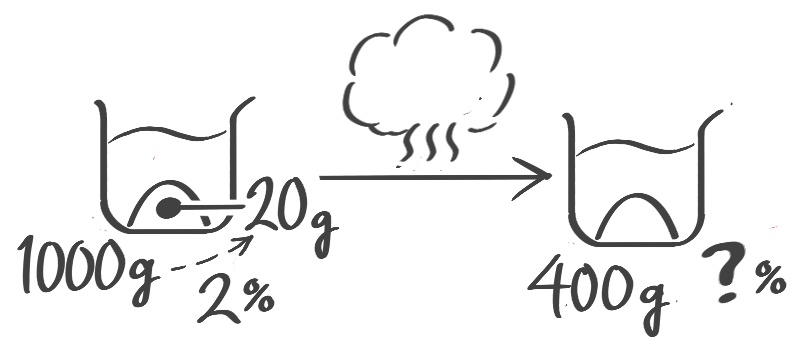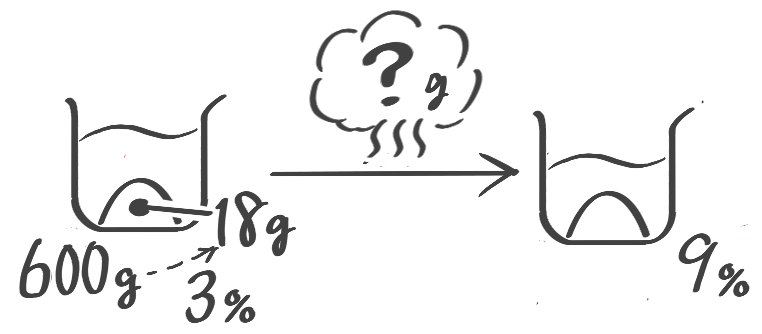「予習シリーズ」を使っている小5の中学受験生の方へ
この記事では東大卒講師歴20年超の図解講師「そうちゃ」が予習シリーズ5年(上)の第6回「濃さ(濃度算)」を分かりやすく図解します
テキストの分からない問題の図解を「テキスト問題へのリンク」からジャンプして見るのも良し、初めから読んで基礎からステップアップしながらじっくり理解するのも良し、自由に使って実力アップに役立てて下さい！
はじめに(ヨリシスについて)
ヨリシス by そうちゃ式
講師歴25年の図解講師「そうちゃ」が、予習シリーズ(が理解させようとしている学習体系)をスルッと理解できる「ヨリシス (Yo-Resys) by そうちゃ式」を始めます♪
予習シリーズベースで学習している小学5年生で「算数が難しい！」テキストが良くわからない…」と悩んでいる方へそれ、当然の悩みです。予習シリーズは分かりやすいテキストなのですが、4年の途中からだんだん難しくなり5年になると4年内容が前提となるので、1回分の内容は4年の最初と比べると3倍くらい！(マジで)
本来「4年内容の復習→5年内容の導入→定理公式の使い方→例題→標準問題→応用問題」という順番で学習するのが望ましいのに、授業がいきなり例題や標準問題からはじまってしまうと算数が苦手な生徒さんは「ぜんぜん分からない！」となってしまいます(涙)
もちろん、予習シリーズには「復習パート」があるのですが、その量が十分でなく、また例題なしの「いきなり標準問題」や標準問題なしの「いきなり応用問題」もあって、算数が苦手な生徒さんが「予習シリーズ」本体を十分に時間をとって予習しても完全に理解するのは難しいです。
じゃあどうすればいいの…と思ったあなた、お任せ下さい
「ヨリシス」について
「ヨリシス by そうちゃ式」は、算数が苦手な人でも理解しやすいように「予習シリーズ」の中身を並べ替えて(再体系化=リシス)そうちゃの図解を加え、さらに例題・問題の前後や途中に前提となる事柄や4年の復習を「補完例題」「補完問題」として追加したものです
算数が苦手な人でも、つまづいた例題・基本問題・練習問題の前にある「補完問題」を学習すれば、つまづきが解消して練習問題も解けるようになるでしょう。
「ヨリシス」の見方
例題,基本問題,練習問題
→「予習シリーズ」掲載の問題
番号に「’」がついているもの(ダッシュ版)は改題/自作バージョン
ダッシュ版には問題とそうちゃ式の図解がついていますが、ダッシュなしの原本版は著作権保護のため問題文は非掲載で図解のみです。
(例題はできるだけダッシュ版にして問題を掲載しています)
補完例題,補完問題→予習シリーズの例題や問題だけでは理解が難しい場合に、前提事項を基本解法を補うために追加したものです。
分からない問題の前に「補完」がある場合は、まずそちらを読むと良いでしょう♪
学習ガイド
テキストの補習に
各回のはじめに例題(類題)・基本問題・練習問題へのリンクである「問題目次」があります。
テキストを学習していて分からない例題・基本問題・練習問題がはっきりしている場合は、各回最初にある「問題目次」からそうちゃ式の「図解」へとジャンプして下さい
算数が苦手でない人は図解を見て理解できたら、ノートまたは「そうちゃ式ワーク(予リシス)」で自分でも書けるか試せば良いでしょう。
算数が苦手な人は、いきなり図解を見るよりは、その前にある「補完問題」を十分に理解(復習)して、それから図解を学習しましょう。「補完問題」も分からない場合は「そうちゃ式1号館/2号館」の該当記事へジャンプして学習して下さい。
テキストの予習に
算数が苦手な生徒さんは4年の範囲を完全に忘れていることが珍しくありません。授業の前に「ヨリシス by そうちゃ式」で各例題の前にある「補完問題」を解けるようにしておくと4年範囲が復習できて授業が分かりやすくなるでしょう。
テキストの代わりに
塾なしで予習シリーズをベースに学習していて、算数が苦手な人は予習シリーズの代わりに「ヨリシス by そうちゃ式」で学習しても良いでしょう
また講習期間などにテキストを予習・復習したい人も予習シリーズ本体よりも「ヨリシス by そうちゃ式」のほうが学習しやすいと思います。
「ヨリシス」総目次(リンク)
4(上)
4(下)
5(上)
1「約数と倍数」/2「面積の求め方」/3「割合」/4「差集め算(&過不足算)」/5「総合」
6「濃度」/7「売買」/8「多角形の回転/転がり」/9「円の回転/転がり」/10「総合」
11「並べ方」/12「組み合わせ方」/13「速さとグラフ」/14「水量変化」/15「総合」
16「旅人算とグラフ」/17「色々な旅人算」/18「数列と数表」/19「点の移動」/20「総合」
5(下)
テキスト問題へのリンク
解き方・解説がよく分からない問題の解説を見たい人はこちらから図解へジャンプして下さい。算数が苦手な人/解説がよく分からない人は、リンク先から少し上にある前提になる問題を見ると理解しやすいでしょう♪
(本回)
◆例題[1(1)/(2)/(3)//2(1)/(2)/(3)//3(1)/(2)
4//5(1)/(2)//6(1)/(2)//7]
◆基本問題[1(1)/(2)/(3)/(4)/(5)/(6)/(7)/(8)/(9)
2(1)/(2)//3(1)/(2)//4//5]
◆練習問題[1(1)/(2)//2//3//4(1)/(2)/(3)//5//6]
==================
(総合回:10回)
今回の学び方
今回はテキストに線分図しか載っていないのが理解をさらに難しくすると予想して、実体図に近く初学者に分かりやすい「ビーカー図」をフィーチャーして、基本公式や考え方から応用問題までスモールステップでレベルアップできるよう、補完に重点をおいて再体系化(リシス)をしました。
記事を通して読みながら図を真似すれば、予習シリーズの原作者が伝えたい内容を体系的に理解する「体験」ができます。
なお「予習シリーズ」に限定せず「そうちゃ式」の体系で最初から学びたい人は関連記事「濃度算まとめ」を見て下さい
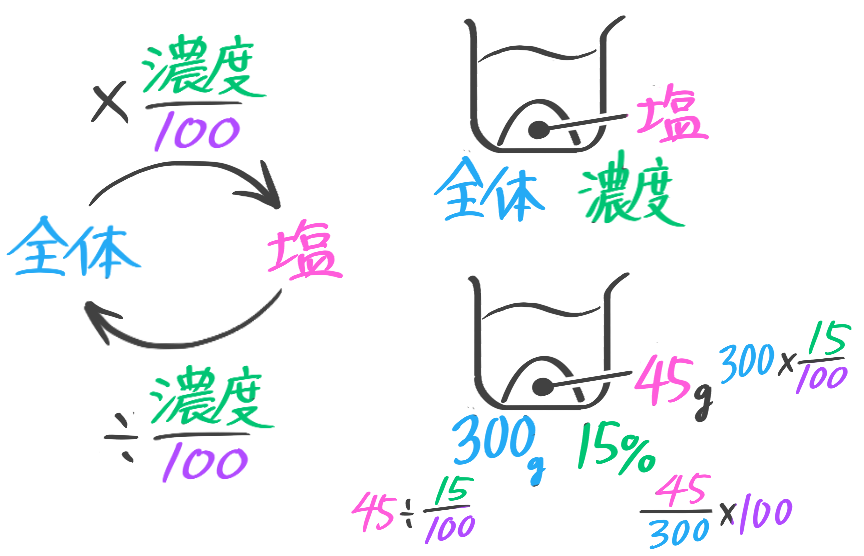
「濃度」とは
日常生活で「～水」を作ったことの無い生徒を念頭に公式に出てくる言葉の理解を確認する。
「～水」の作成
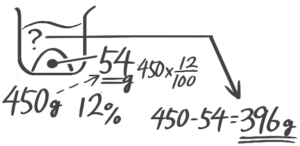
例題000-1
水450gに塩50gを溶かして食塩水を作る以下の問いに答えなさい
(1)「全体の重さ」は何gになるか
450+50=500g
(2)食塩水全体に占める塩の重さの割合はいくつか
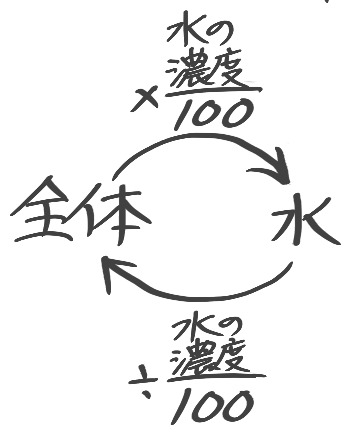
矢印図を思い出して
この場合、食塩水全体が「元の数」で塩の重さが「先の数」になると考えて、
全体→(割合)→塩
割合＝塩÷全体=50÷500=0.1(1/10)と分かる
(3)食塩水全体に占める塩の割合を百分率で表わせ
割合(小数)を100倍(小数点を左に2ｹﾀずらす)したのが百分率だったから、
この場合は、0.1×100=10%と分かります。これが食塩水の「濃度」になります。
(全体像)
「水」に「塩」を溶かして食塩水を作る。
「塩」が食塩水「全体」に占める割合(塩÷全体)を100倍したのが「濃度」である
例題000-2
こんどは水450gに塩450gを溶かして食塩水を作った。以下の問いに答えなさい
(1)塩の割合は
(2)濃度は
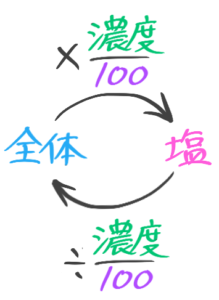
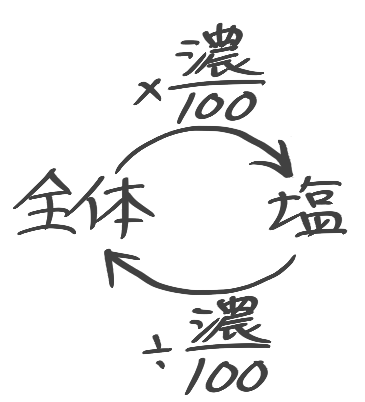
濃度の基本公式
濃度の三公式
以下の問いに答えなさい
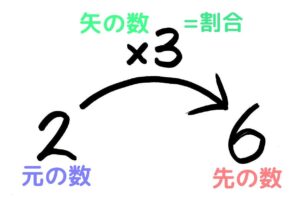
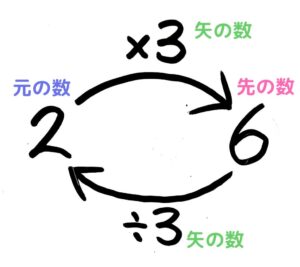
(1)2,3,6が「2×3=6」の関係にある図(矢印図)を書きなさい
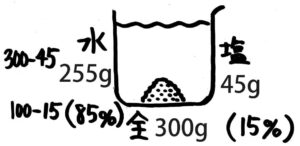
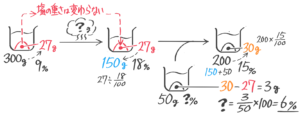
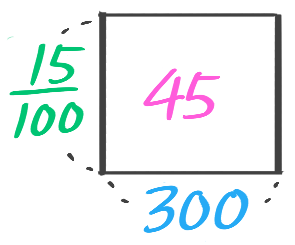
(2)□を埋めなさい「濃度15%の食塩水300gに含まれる塩の重さは、300gの15%つまり300x□=□gである」
(3)「食塩水全体の重さ(全体)」「塩の重さ(塩)」の関係を「矢印図」にしなさい
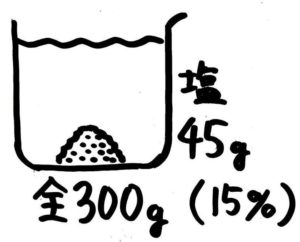
(4)食塩水全体300g,塩45g,濃度15％をビーカー図にしなさい
(5)「全体」「塩」「濃度」の求め方を公式にしなさい
「2」「x3」「6」を矢印で結んだものが「矢印図」
２を「もとの数」ｘ３を「矢の数」６を「先の数」と呼び、矢の数が割合になっています。
発展形は逆向きの矢印をつけます。逆向きは割り算になります。
割合全ての基本が「矢印図」です。迷ったらここに戻りましょう
「濃度15%の食塩水300gに含まれる塩の重さは、300gの15%つまり300x0.15=45gである」
15%は0.15よりも分数(15100)にした方が約分ができてラクです♪
(2)の「全体x濃度100=塩」を矢印図にします
「矢の数」は「濃度」ではなく「濃度100」になることに注意
食塩水が入ったビーカーをイメージした図が「ビーカー図」です
左下に食塩水全体の重さ(全体)、右下に濃度、右に塩の重さ(塩)を書きます。このように書く理由は、この後分かります
濃度の3つの公式はこうなります。
濃度=塩全体×100
塩=全体×濃度100
全体=塩÷濃度100
純粋な割合でなくパーセントを使うので、「100」が出てくるのに注意しましょう
ビーカー図の「全体」「濃度」「塩」が「矢印図」と同じ順になっていて、ビーカー図は「矢印図」の一種と分かりますね
分かりましたか？
理解できたら、公式が早口言葉のスピードで暗唱できるまで練習して下さい
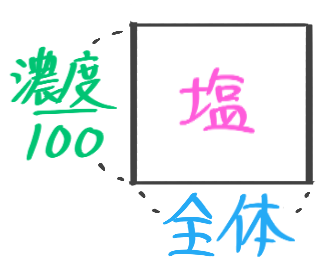
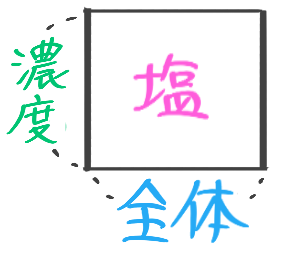
➊濃度=塩全体×100
❷塩=全体×濃度100
❸全体=塩÷濃度100
濃度の問題では、まずビーカー図を書いて計算できることはしてしまいます。考えるのは、その後です。
公式の練習
ビーカー図を書いてから三公式そのものを使う練習
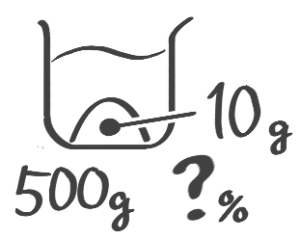
濃度を出す
食塩10gを使って500gの食塩水を作ると濃度は何%か
問題文の「塩10g」「全体500g」をビーカー図に書く。聞かれている濃度は「？」にする
公式「濃度=塩全体x100」を使って、濃度は2%と求められる
x100を忘れないこと！
[基本問題1(1)]
補完例題1-2(1)↑参照
塩の重さを出す
3%の食塩水400gには食塩が何gとけていますか
問題文の「濃度3」「全体400」をビーカー図に書く。聞かれている塩は「？」にする
公式「塩=全体x濃度100」で塩は12gと求められる
[基本1(3)]
例題1(2)↑参照
全体の重さを出す
塩4.8gが入っている4%の食塩水は何gになるか
問題文の「濃度4」「塩4.8」をビーカー図に書く。聞かれている全体は「？」にする
公式「全体=塩÷濃度100」で食塩水全体は120gと求められる
[基本問題1(5)]
補完例題1-1(2)↑を参照して下さい
公式を工夫する
三公式では「水」を直接は求めないが「塩+水=全体」という関係から間接的に求めることができる
水と塩から濃度を出す
170gの水に30gの食塩を溶かすと何%の食塩水ができますか
「水の重さ170」はビーカー図の塩の「山」の上のあたりに書き、求める濃度は「？」にする
全体の重さ=塩+水なので200と分かる。
全体と塩が分かれば、公式「濃度=塩全体x100」で濃度も15%と求められる
[基本問題1(2)]
例題1′(1)↑を参照
水の重さを出す
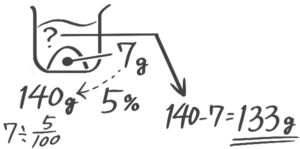
7gの食塩を何gの水に溶かすと5%の食塩水ができますか
「濃度7」と「塩7」をビーカー図に書く
公式「全体=塩÷濃度100」で全体=140gと出して、
塩7gを引けば水133gと求められる
[基本問題1(6)]
例題1′(3)↑を参照
(4)’ 12%の食塩水450gを作るには水と食塩がそれぞれ何g必要か
ビーカー図に「濃度12」「全体450」「塩？」を書く
基本公式「塩=全体x濃度100」から塩を54gと出して
全体450gから塩54gを引いて、水=396gと求められる
[基本問題1(4)]
基本問題1(4)’↑を参照して下さい
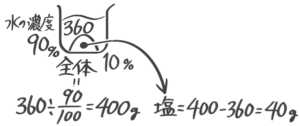
水から全体を求める
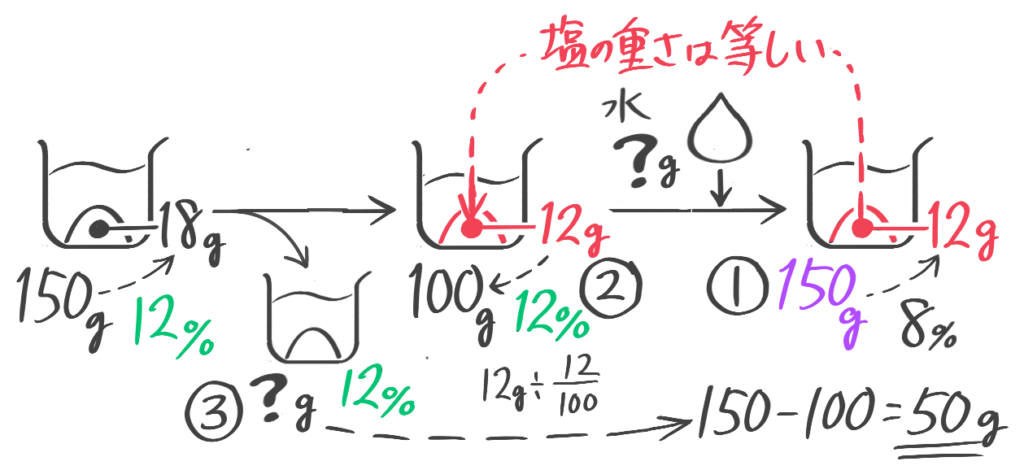
水360gで10%の食塩水を作るには塩を何g入れればよいか？
ビーカー図に「水360」「濃度10」「塩？」を書くが
水と濃度を使った公式は知りませんね…そこで「水の濃度」を考えます！
全体100%のうち塩が10%なので残りの90%が水ですね。この90%が「水の濃度」です
水360gが全体の90%なので、全体は 360÷90100=400g 、塩は 400-360=40g と求められます
水の濃度を加えた発展ビーカー図は下のようになります。
そして公式にするとこうなります
➊水の濃度=100－塩の濃度
❷水の重さ=全体の重さ－塩の重さ
❸全体の重さ=水の重さ÷水の濃度100
基本の三公式を覚えた人は、こちらも「作れる」ようにしておきましょう。
(問題は省略。テキストを参照して下さい)
ビーカー図に水の重さを書きます
「水の濃度」は100ー塩の濃度20=80%
水の重さ400と水の濃度80%から全体の重さは500gと求められる。
次に、塩の濃度20%と全体500gから塩の重さも100gと求められる
要素の増減
完成した食塩水に水や塩を増やしたり、水を蒸発させて減らしたりします。
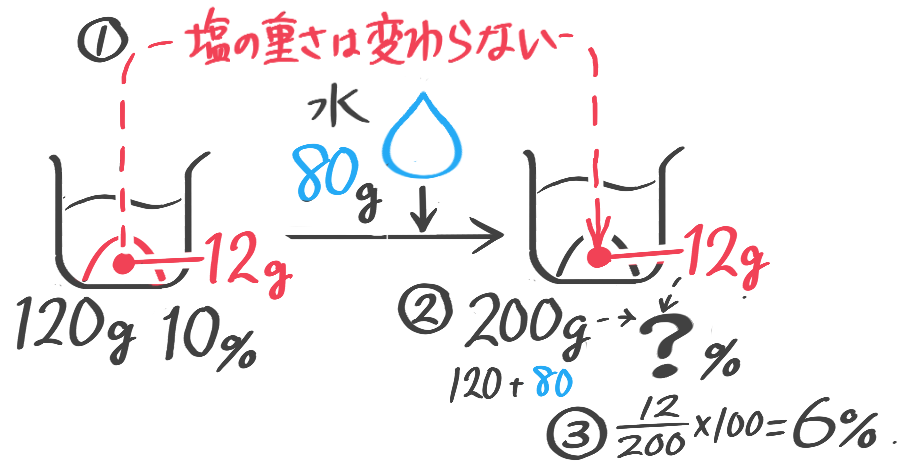
❶2つのビーカー図をつなげた絵を書いて考えます
❷増えたり減ったりしていないモノに注目する
加水
水を加えても塩は変わらないことに注目する
加水後の濃度を求める
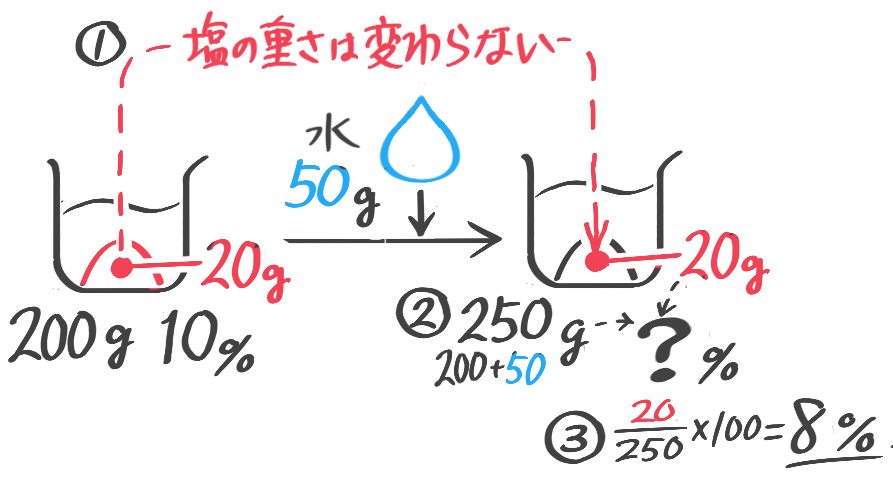
10%の食塩水120gに水を80g加えると何％の食塩水になりますか
まずAの塩の重さを 120x10100=12g と出してBe数に書いておく
加水前の食塩水全体が120gで加えた水が80gなので、加水後の食塩水全体は200g。塩は変わらず12g。
ここで「濃度=塩全体x100」の公式を使って、加水後の濃度は12200x100=6%と求められる。
(7) 10%の食塩水200gに水50gを加えると何%の食塩水になるか(問題文章は省略。テキストを参照して下さい)
ビーカー図を書くときに塩の重さは 120x10100=12g と出しておく
水を加えても塩の重さは変わらず20g。全体の重さは50g増えて250gになる
全体250,塩20より濃度は8%と求められる
加水量を求める
9%の食塩水に120gに水を何g加えると3％の食塩水になりますか
塩の重さは120x9100=12 x 910=10.8(あとで約分するので、わざと分数にしておいても良い)
水を加えた後も塩の重さは変わらず、濃度は3%なので、全体の重さは「全体=塩÷濃度100」の公式を使って=360gと分かります。
水を加える前が120g、後が360gなので、加えた水は360-120=240gです。
[基本問題2(1)]
例題2′(2)↑を参照
初めが分からない場合
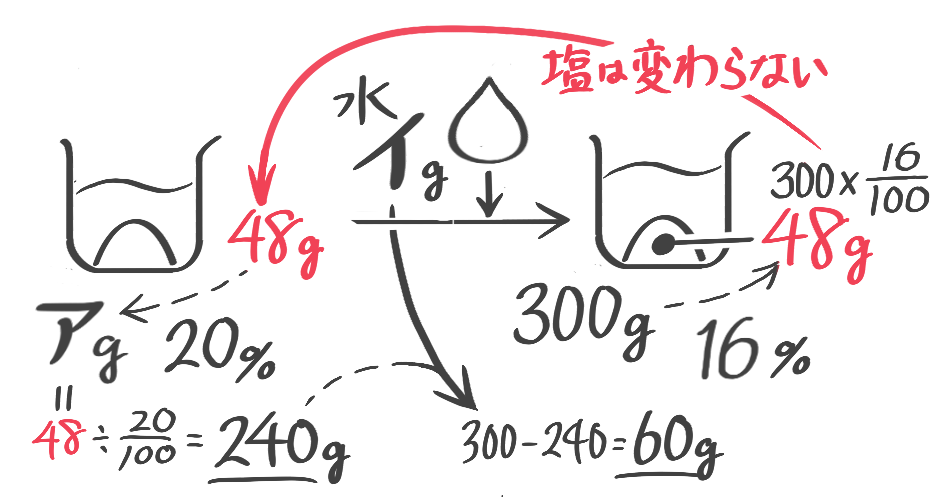
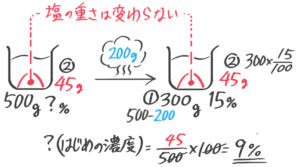
(1) 20%の食塩水が何gかある。これに水を加えたところ16%の食塩水300gになった。最初の重さと加えた水の重さを求めよ(問題省略。テキストを見て下さい)
ビーカー図で状況をつかむ
加水後の塩=加水前の塩を求めれば、加水前の全体が240gと分かるので
加えた水の重さも60gと求められる
減水
熱して水だけを蒸発させて減らす。塩の重さが変わらないことに注目する
後の濃度を求める
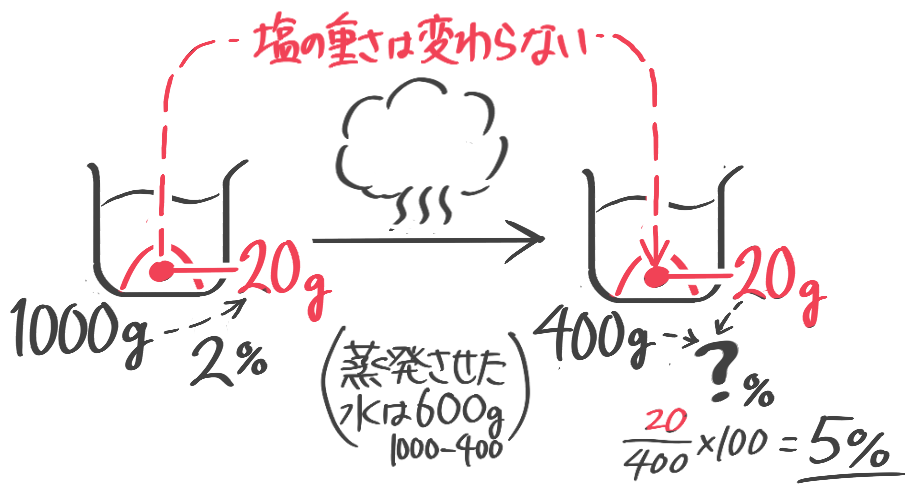
2%の食塩水1000gを煮て400gにすると濃度は何%になるか？
まずAの塩の重さを、1000x2100=20g と出してビーカー図に書き込んでおきます
煮詰めた後の食塩水が400g、塩は変わらず20gなので、後の濃度は、濃度の公式「濃度=塩全体x100」を使って20400x100=5%です。
[基本問題1(8)]
補完例題2-1(1)↑参照
蒸発させる水量を求める
3%の食塩水600gから水を何g蒸発させると9%になりますか
塩の重さを 600x3100=18g と求めてビーカー図に書き込んでおきます。
水を蒸発させた後も塩の重さは変わらず18g、濃度は9%なので、蒸発させた後の全体の重さは「全体=塩÷濃度100」の公式を使って、18÷9100=200gと分かります。
水を蒸発させる前が600g、後が200gなので、蒸発させた水は600-200=400gです。
(1) 9%300gを15%の食塩水にするには水を何g蒸発させればよいか(問題省略。テキストを参照して下さい)
状況をビーカー図にする
蒸発前の塩=蒸発後の塩を出して
公式で蒸発後の全体を出せば、蒸発した水の量も分かる
前の濃度を求める
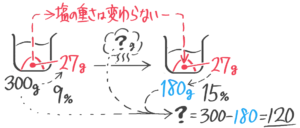
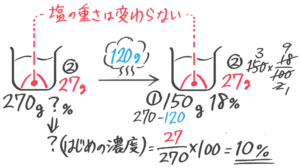
濃さが分からない270gの食塩水から水を120g蒸発させたところ18％になった。はじめの濃度は何％だったか
問題文の状況をビーカー図にする
蒸発させた後の全体は270120=150gなので塩の重さは150×18//100=27と分かる。
そして塩の重さは水を蒸発させる前も変わらず27gなので、濃度は27//270×100=10%と分かります
(2)濃さの分からない食塩水500gから水200gを蒸発させたら15%になった。はじめは何%だったか (問題省略。テキストを見て下さい)
ビーカー図を書きます
全体の重さが300gに減った全体の重さと濃度15%から塩の重さは45gと分かります
そして塩の重さは減水前も変わらず45gなので、全体500gと合わせて、濃度は9%と求められます。
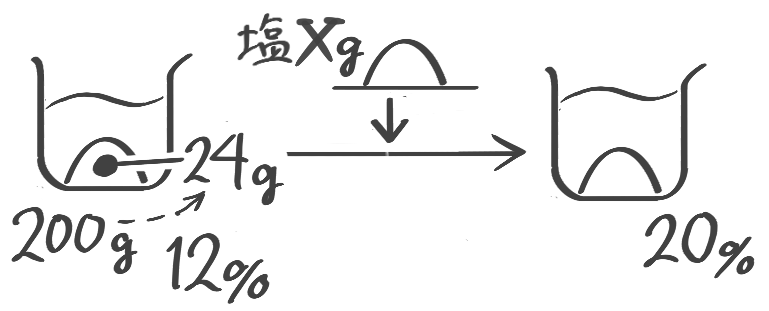
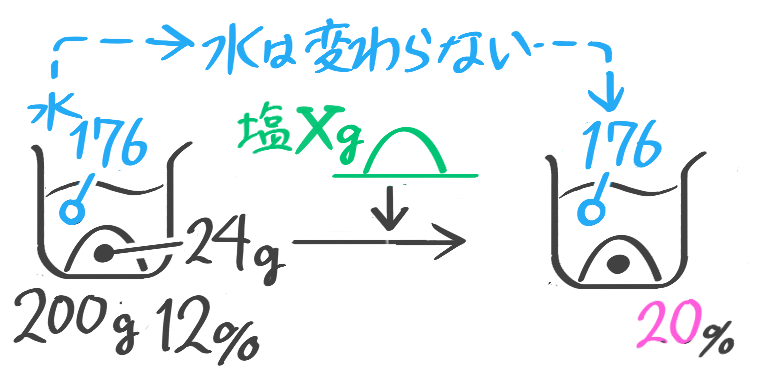
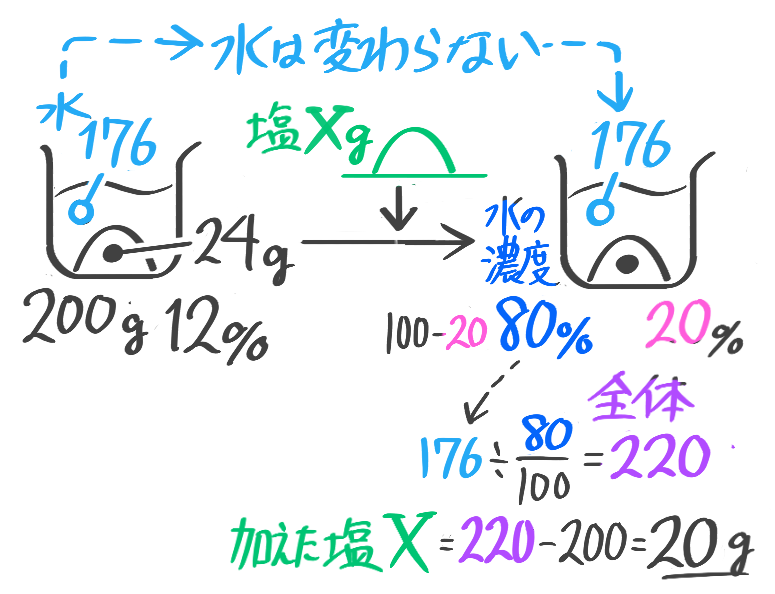
加塩
塩の場合は「増やす」しかありません。変わらないのは水ですが…
濃度を求める
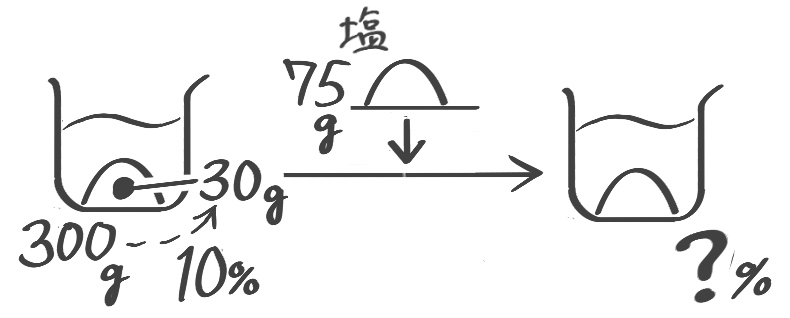
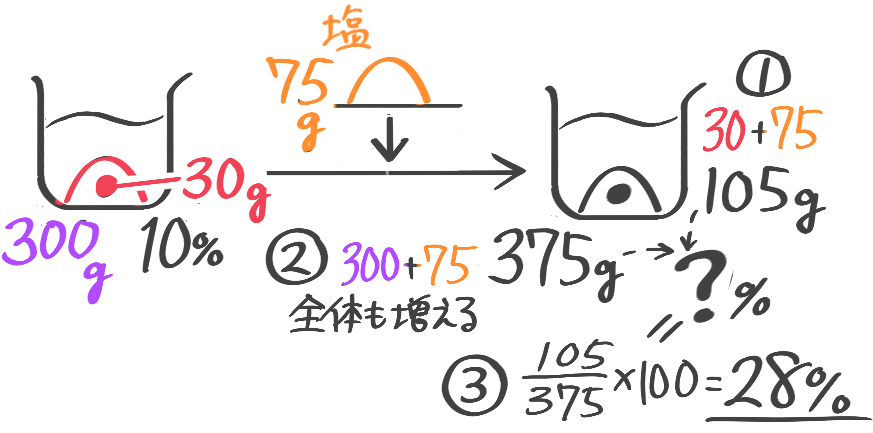
10%の食塩水300gに食塩を75g加えると何%の食塩水になりますか
ビーカー図に初めの塩 300x10100=30g を書き込んでおきます。
ここに塩75gを加えると、全体は375g、塩は105gに増えるので(全体も増えることに注意！)、
濃度=105375x100=28%と求められました。
[基本問題1(9)]
例題3′(1)↑を参照して下さい
加えた塩を求める
こちらは基本公式だけでは難しいので一工夫必要です
12%の食塩水200gに食塩を何g加えると20%の食塩水になりますか
初めの塩の重さ24gをビーカー図に書きます
水の重さが変わらないので、水の重さを書き込みますが
基本公式ではこれ以上計算ができそうにありません。そこで、上で使った水の濃度の公式をつかいます。
➊水の濃度=100－塩の濃度
❷水の重さ=全体の重さ－塩の重さ
❸全体の重さ=水の重さ÷水の濃度100
はじめの水の量200-24=176gは塩を混ぜた後も変わらず、濃度が20%になると「水の濃度」は100-20=80%になるので、
塩を加えた後の全体=176÷80100=220gで、加えた塩は220-200=20gと分かりました。
1回混合
「やりとり算」と同じで、混ぜる前後で塩の重さ,全体の重さの合計は変わらないのを利用できると簡単に解けますが…
基本混合
登場するビーカー3つのうち、2つの重さが分かっている場合は、ビーカー図を丁寧に書いていけば解けます。
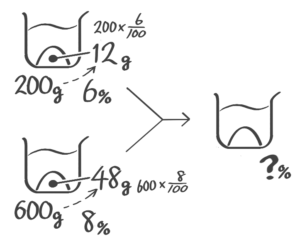
混合後の濃度を求める
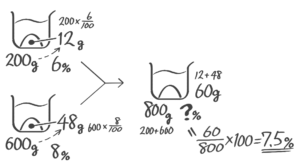
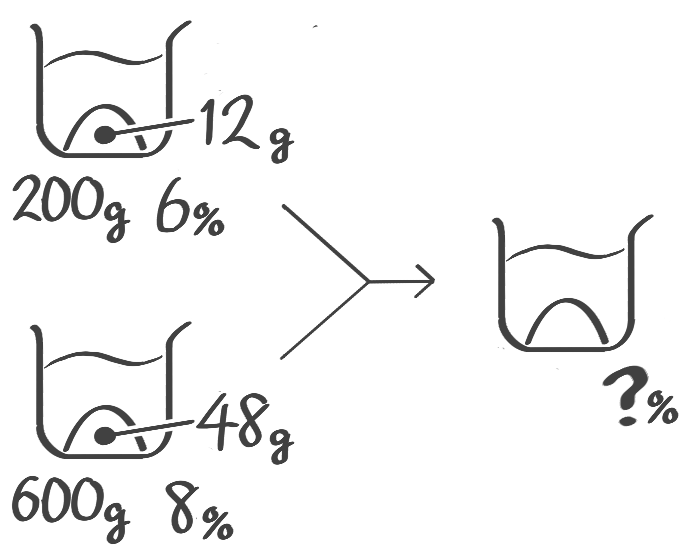
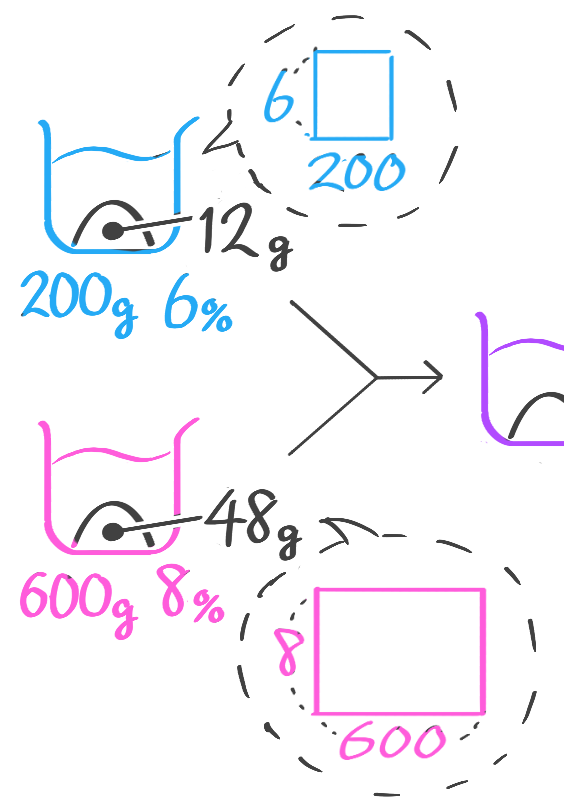
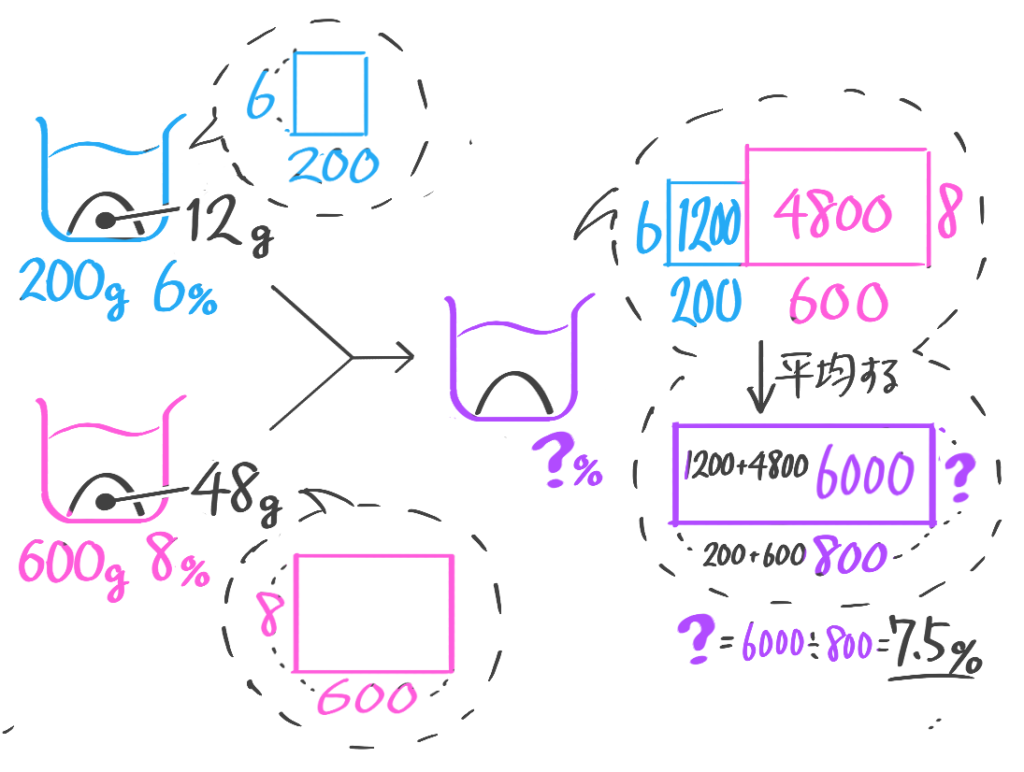
6%の食塩水200gと8%の食塩水600gを混ぜると何％の食塩水になるか
ビーカー図を書きながら塩の重さを出すと、12gと48gなので、
混ぜ合わせてできるのは全体の重さが200+600=800g、塩の重さが12+48=60g の食塩水なので、
濃度は60800x100=7.5%と分かります。
[基本3(1)]
例題5′(1)↑を参照して下さい
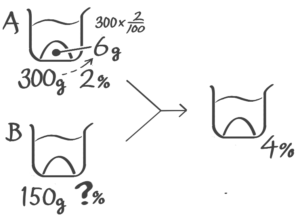
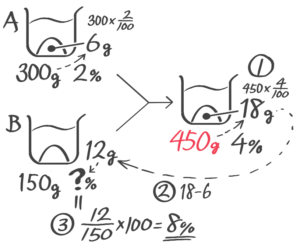
混合前の濃度を求める
濃さが分かっていない食塩水が150gあります。この食塩水に2%の食塩水を300g加えたところ、4%の食塩水になりました。はじめの食塩水の濃さは何%でしたか
2%の食塩水の塩を出しながら、ビーカー図を書きます
合わさった食塩水の全体は450gなので塩の重さは18gです
そこから「さかのぼって」150gの食塩水に含まれていた塩が18-6=12gと分かるので、濃度も8%と求められます
[基本問題3(2)]
例題5′(2)↑を参照して下さい
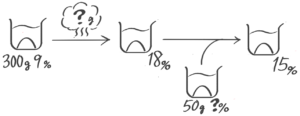
連続作業
2回混合をしたり、混合の前後に作業がある問題
(2) 9%の食塩水300gを加熱して水を何gか蒸発させて15%にしたかったが、加熱しすぎて18%になった。そこで濃さの分からない食塩水50gを加えたところ15%にできた。何%の食塩水を加えたか(問題は省略。テキストを参照して下さい)
ビーカー図で状況をつかみます。
前半の作業で18%の食塩水150gになり、後半の作業で15%300gの食塩水になると分かるので、
基本混合の考え方で、混ぜた50gの食塩水の中の塩が3g，濃度は6%と分かります。
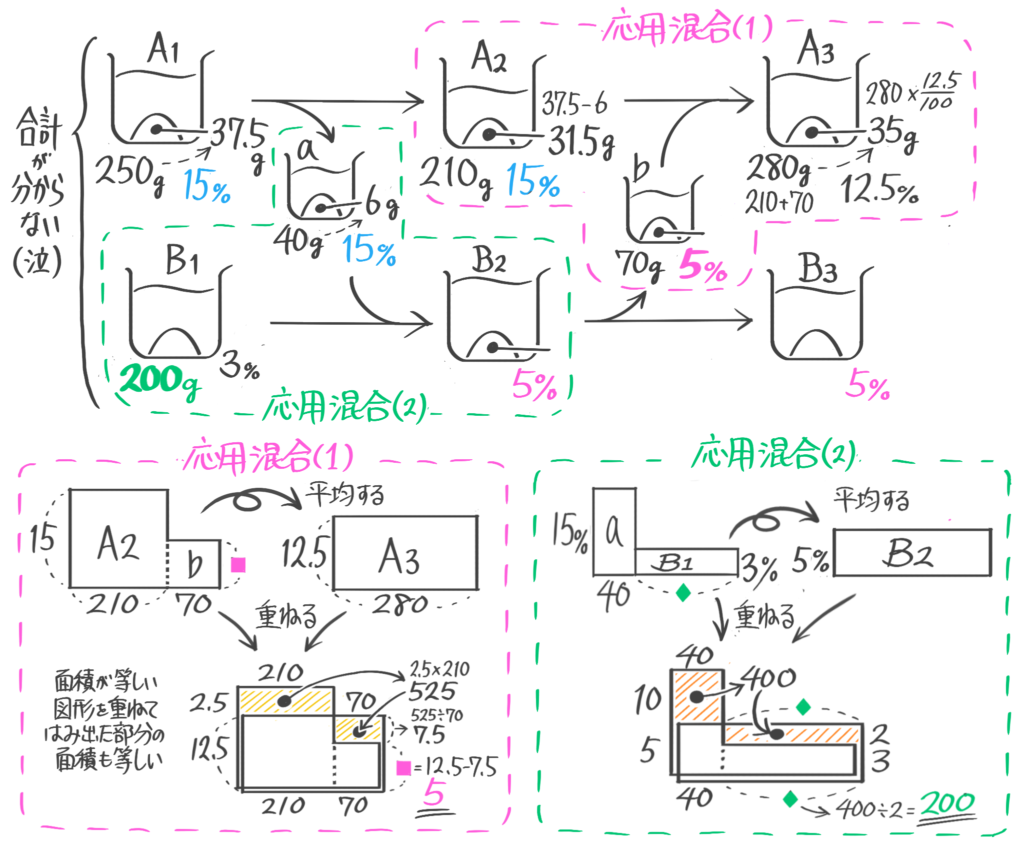
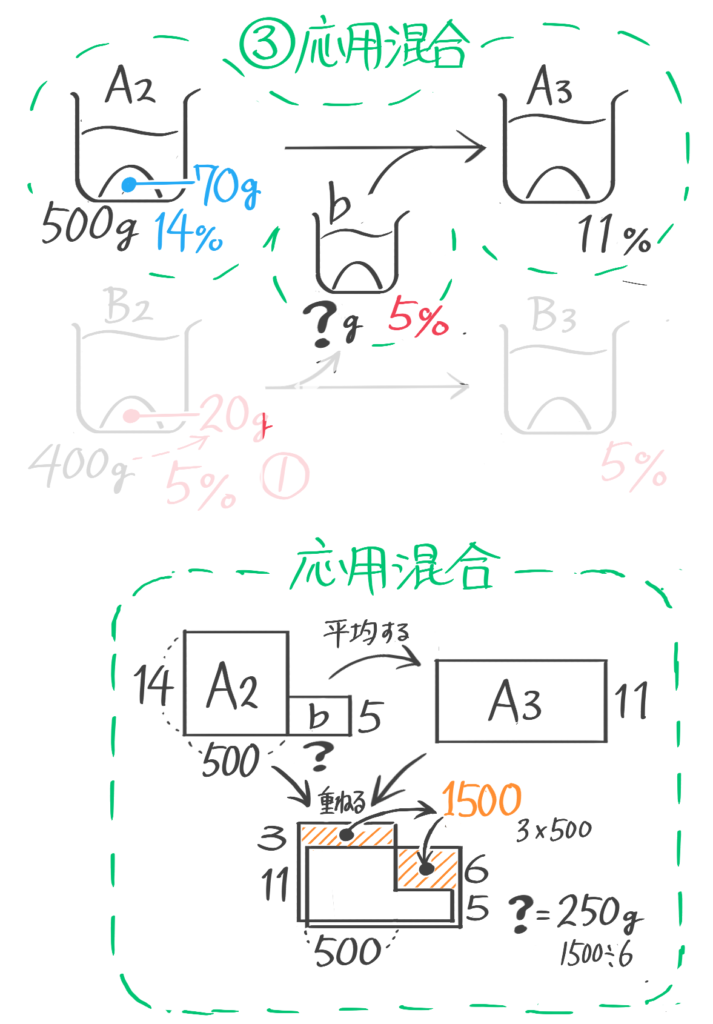
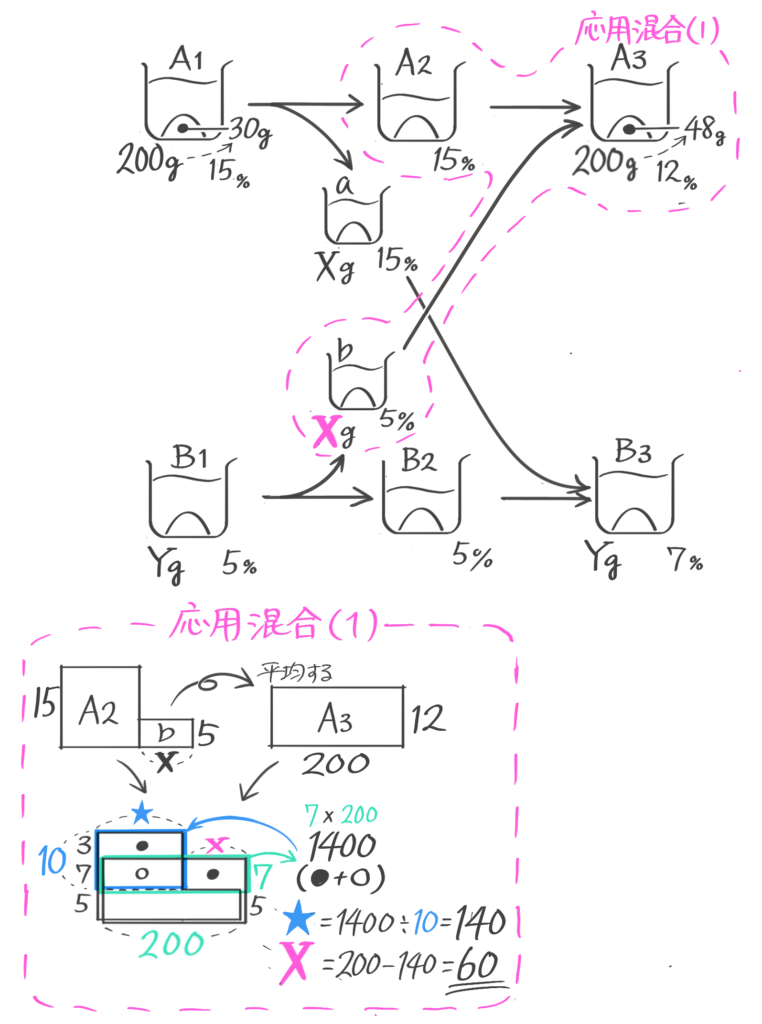
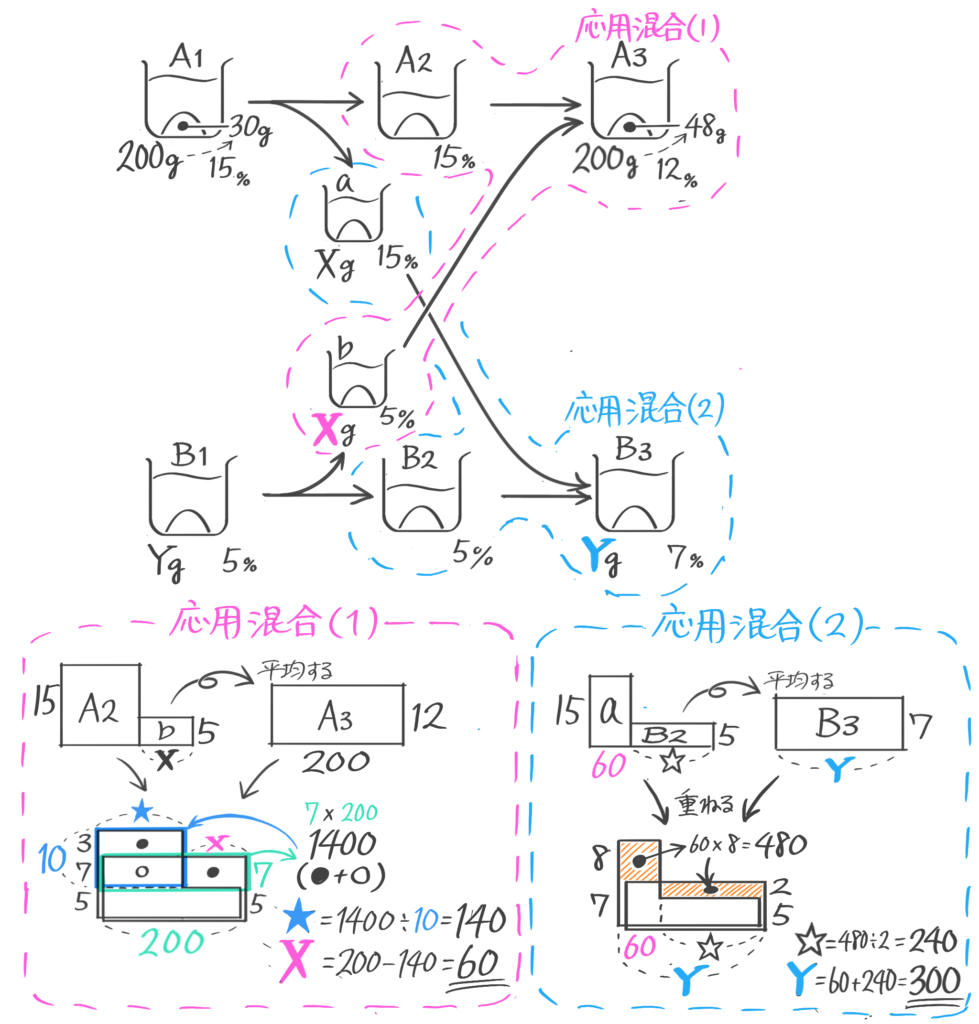
応用混合
混合に登場する3つの食塩水(ビーカー)のうち、1つしか全体の重さが分からない場合、ビーカー図をどんなに丁寧に書いても解けません。そこで応用図(「てんびん図」か「面積図」)を使って解きます。
本来は「比」を学習してから解くべきで「そうちゃ式」でのオススメは「比を使ったてんびん図」なのですが、今回はテキストに従って「比を使わない面積図」での解法を説明します
濃度の面積図
まず濃度の三公式を面積図にしてみます
15%の食塩水300gに入っている塩をもとめ、濃度・全体・塩を面積図にしなさい
塩=全体x濃度100は45gと求められます。
今の公式「塩=全体x濃度100」を「長方形の面積=縦x横」と同じように考えると、全体が横、濃度100が縦、塩が面積の面積図にできます。
この食塩水の場合は、こうなりますね
ただ混合で使う場合は濃度をそのまま縦にしても解けます(後でコチラを使います)。
次に面積図を使ってみましょう
面積図1(はみ出た部分)
混ぜる2つのうちの1つの重さが分かっている場合
まず混合を面積図で表してみましょう
6%の食塩水200gと8%の食塩水600gを混ぜると何％の食塩水になるか、面積図で求めなさい
実は例題5′(1)と同じ問題で、ビーカー図はこうでした
200gと600gの食塩水を面積図にします。濃度をそのまま縦にしています。
くっつけるとL字形の面積図が出来て面積は6000です(これは塩を100倍した数値です)。これを平らにならします。
その高さが混合してできる食塩水の高さです。ここでは6000÷800=7.5%と求められました。
この書き方を使って、いよいよ問題を解いてみましょう！
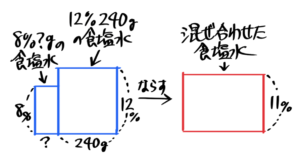
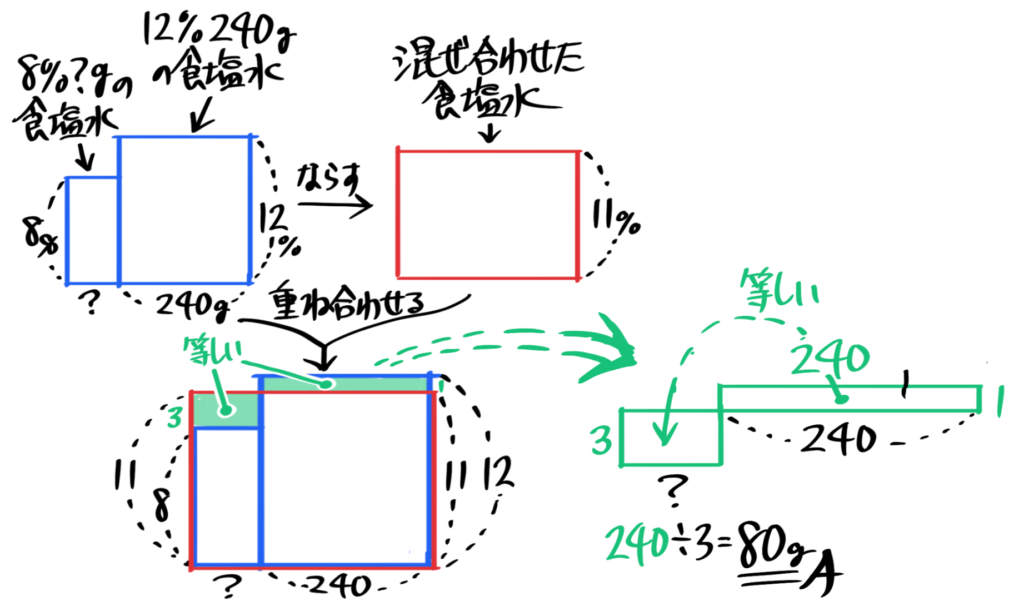
12%240gの食塩水と8%の食塩水を混ぜて11%の食塩水を作ります。8%の食塩水を何g混ぜればよいですか
2つの食塩水の面積図をくっつけてから、平らにならします
以前「等しい面積の図形を重ねると、はみ出た部分の面積は等しい」と学んだのを思い出して…
ならす前と後の図を重ねて、はみ出た部分(緑色の長方形)の面積が等しいことを利用すると
?=80と分かります
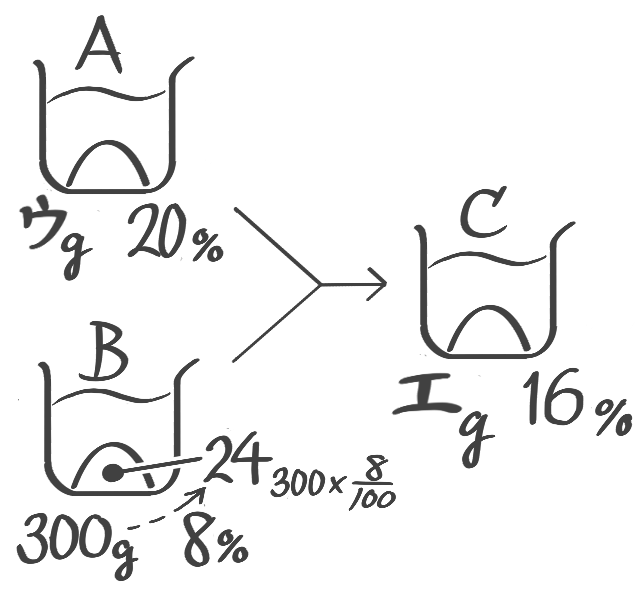
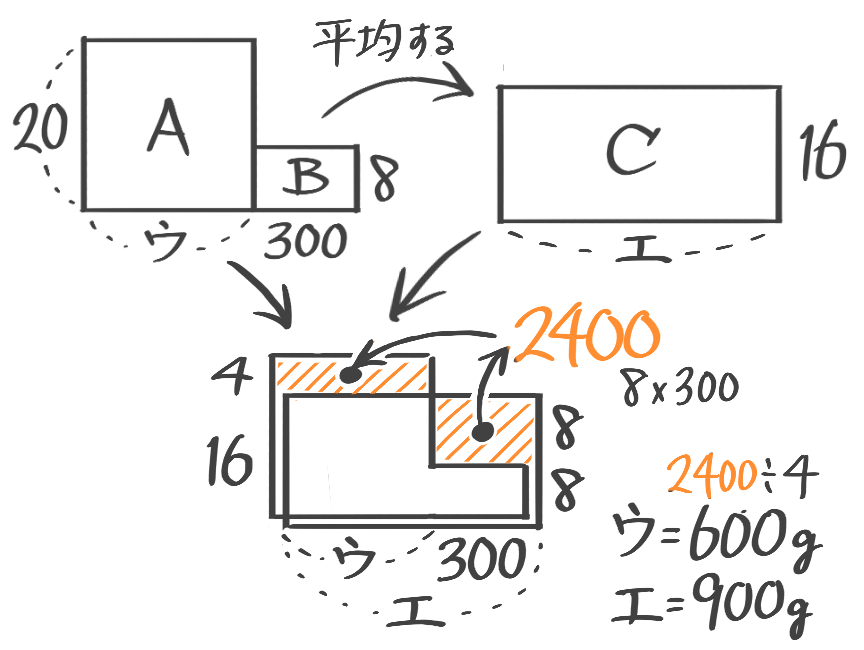
(2)重さが分からない20%の食塩水と8%300gの食塩水を混ぜると16%になった。20%の食塩水の重さと16%の食塩水の重さを求めよ (問題は省略します。テキストを参照して下さい)
ビーカー図を書いて状況をつかむと…
全体の重さが1つしか分からず基本混合は無理と分かるので、面積図を書いて重ねて「はみ出た部分●」が等しいことを利用する
ウが600g,エは900gと求められる
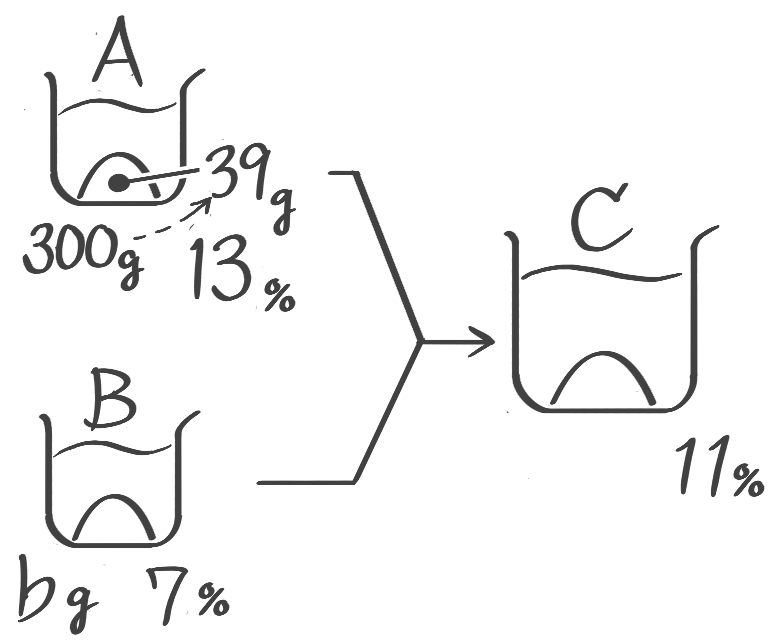
(2)13%300gの食塩水と7%の食塩水を混ぜて11%の食塩水を作る。７％の食塩水を何g混ぜれば良いか(問題は省略。テキストを見て下さい)
描いているうちにビーカー図だけでは解けないと分かる
A+Bの面積図とCの面積図を重ねて、はみ出た部分が等しいことを利用すると、b=150と分かる
面積図2(はみ出た部分+共通部分)
混合で出来た食塩水の重さしか分からない場合「比を使わない面積図」で解くにはさらに工夫が必要です。
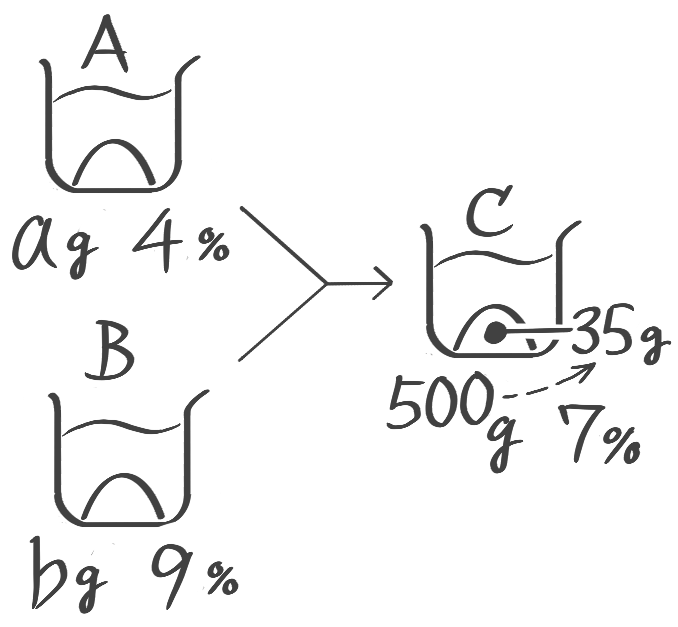
4%の食塩水と9%の食塩水を混ぜて7%の食塩水500gを作ります。9%の食塩水を何g混ぜればよいですか
ビーカー図を書いてみると…これ以上は計算ができないので応用的な図(ここでは面積図)を書きます。
AとBを表す2つの長方形をくっつけたL字形と、それを平らにならした長方形を重ねます
ところが、さっきまでの面積図と違い「はみ出た部分(●)」の面積が出せません。
そこで「○」の部分を共通部分として加え「●+○」が等しいことを利用すると、最初にbが300g、次いでaが200g と分かります。
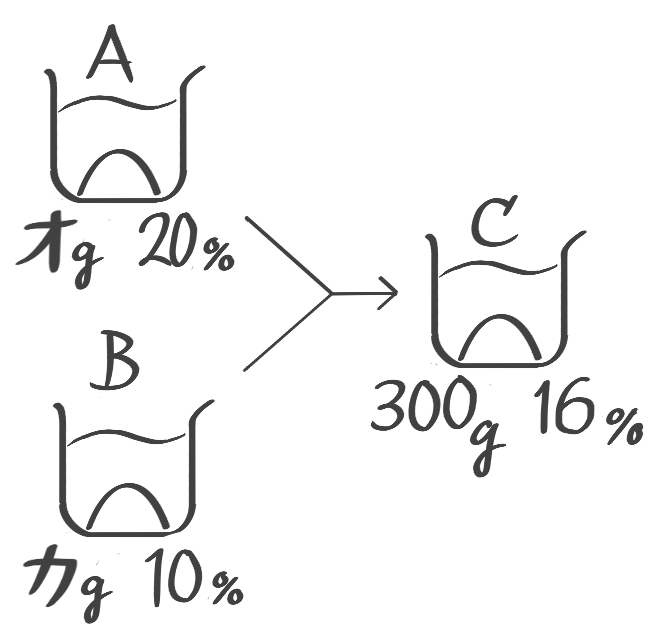
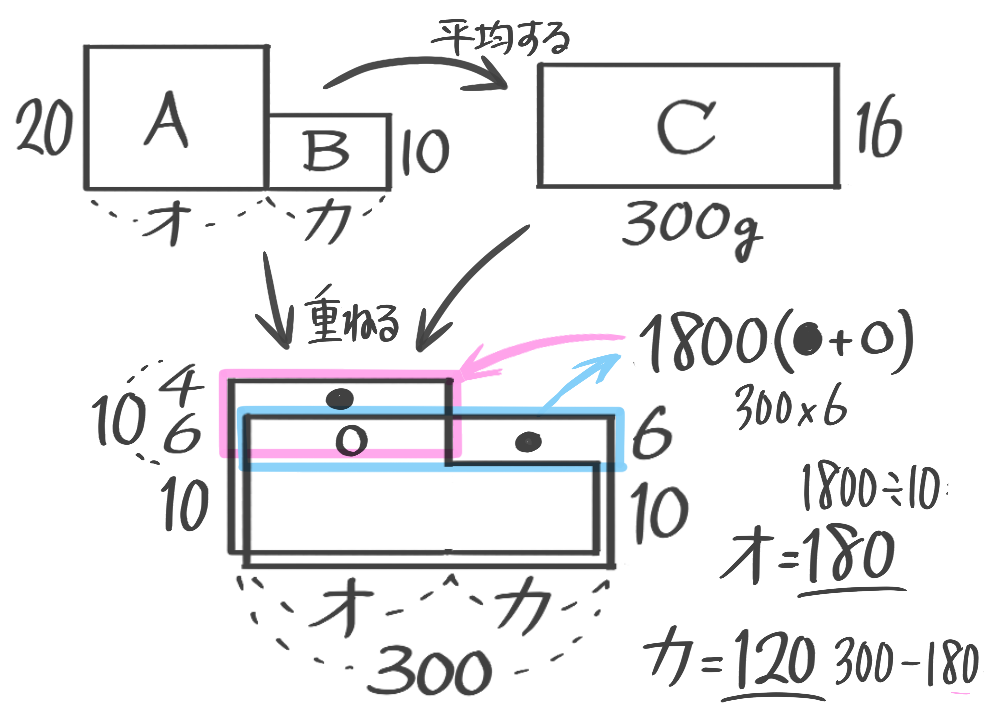
(3) 16%300gの食塩水を作るには20%と10%の食塩水をそれぞれ何gずつ混ぜれば良いか(問題省略。テキストを参照して下さい)
ビーカー図を書くと、基本混合は無理と分かるので応用混合の図(ここでは面積図)を書きます
はじめの食塩水が2つとも重さが分からず「はみ出た部分(●)」だけだと比べることができないので、
「○」の部分を共通部分として加え「●+○」が等しいことを利用すると、最初にオが180g、次いでカが120g と分かります
食塩水の置き換え
食塩水の一部を捨てて、同じ重さの水や他の食塩水を入れます。全体の重さが変わらないのがポイント。まずはビーカー図を書きましょう
[例題4′]
[基本問題4]
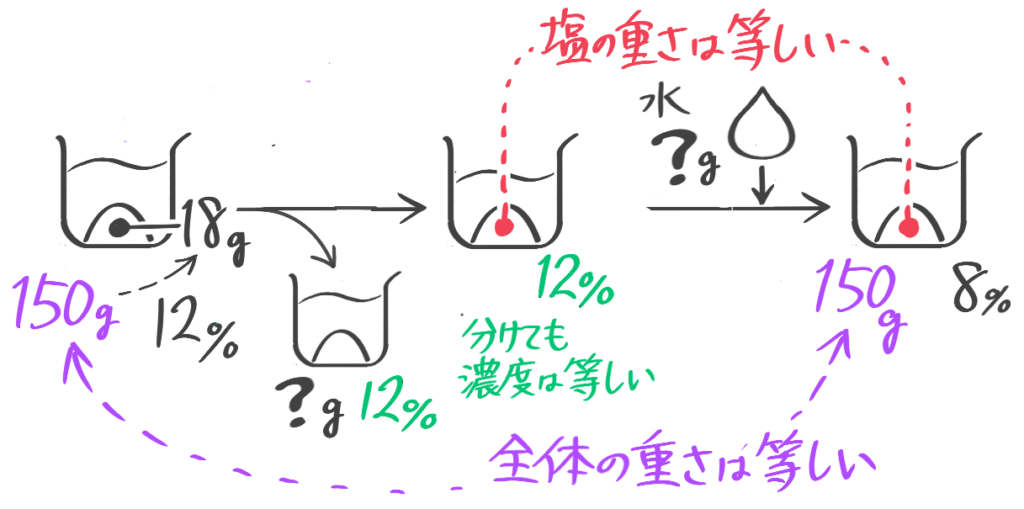
(1)12%の食塩水が150gある。この食塩水を何gか捨ててから、捨てたのと同じ重さの水を加えたところ、8%の食塩水になった。捨てた食塩水は何gか(問題文章は省略。テキストを見て下さい)
置き換えの性質を思い出しながらビーカー図を書く。
分けても濃度は変化しない、水を加える前後で塩の重さは変化しない、さらに「最初と最後の重さは等しい」
最後の状態での「塩」=12を出せば、真ん中の「全体」=100gと分かるので、捨てた重さは50gと求められる
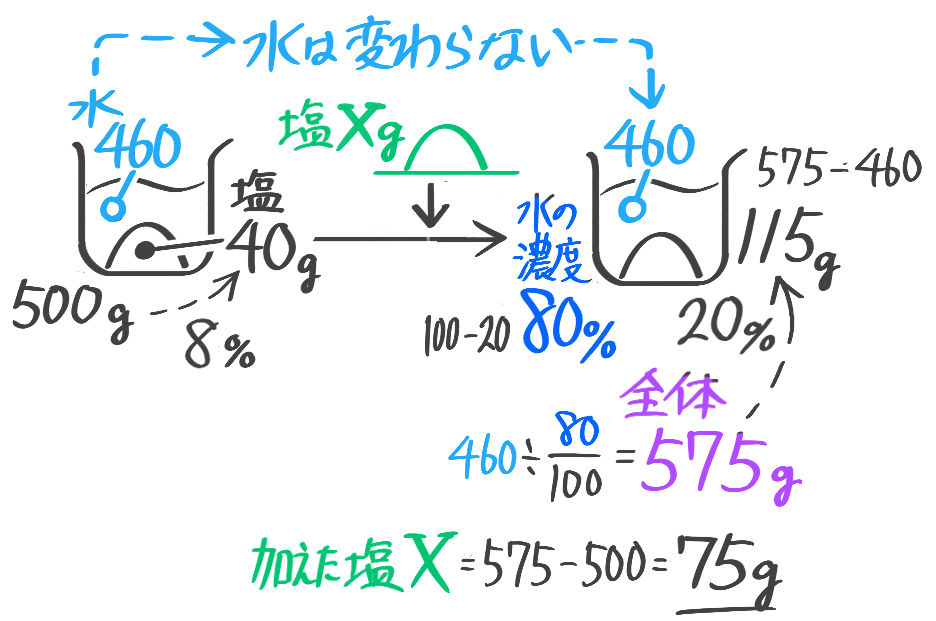
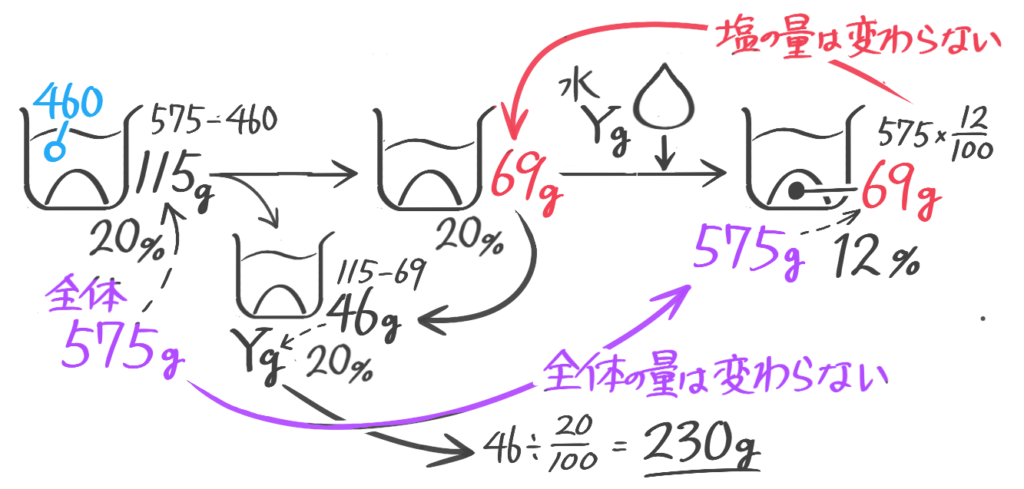
8%の食塩水が500gある。まず食塩を何gか加えたところ20%になった。次にこの食塩水を何gか捨てて、捨てたのと同じ重さの水をくわえたところ12%になった。(1)加えた食塩は何gか(2)捨てた食塩水は何gか(問題文章省略。テキストをみて下さい)
ビーカー図を書いて状況をつかみます
前半は「水の濃度」を使って、加塩後の全体の重さを575gと求めれば、加えた塩の重さも75gと分かる
その後、一部を水に置き換えても全体の重さは変わらないので最後の全体の重さも575gのままで、塩の重さが69gと分かり、これは一部を捨てた直後も変わらない。
これで、小分けして捨てた食塩水の塩の重さが46g(濃度は20%のまま)と分かるので全体の重さYも230gと求められる
(解答の全体像)
食塩水のやり取り
複数の濃度が違う食塩水で「やり取り」をします。まずビーカー図を書けるように練習して下さい
ポイント
①やり取りしても合計(食塩水全体の合計と塩の合計)は変わらない
②食塩水は分けても濃度は変わらない
基本やりとり
ビーカー図を書けば解けるものです。ポイント①「全体や塩の合計は変わらない」を使いましょう
[補完例題7-1]
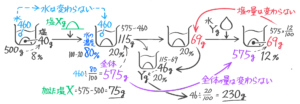
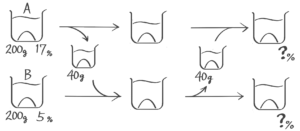
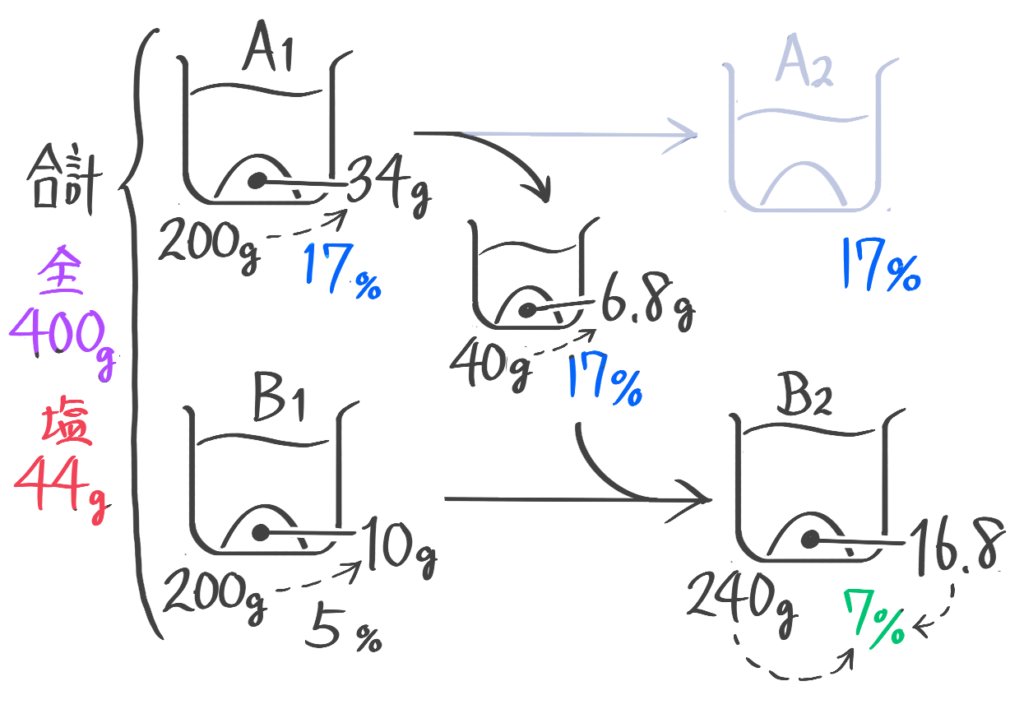
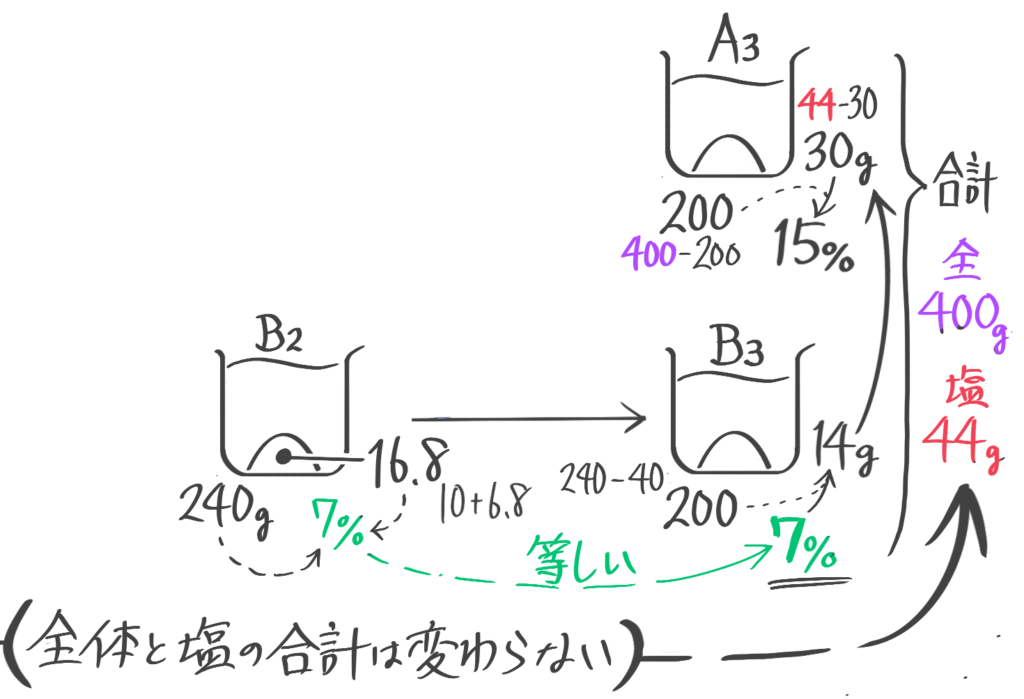
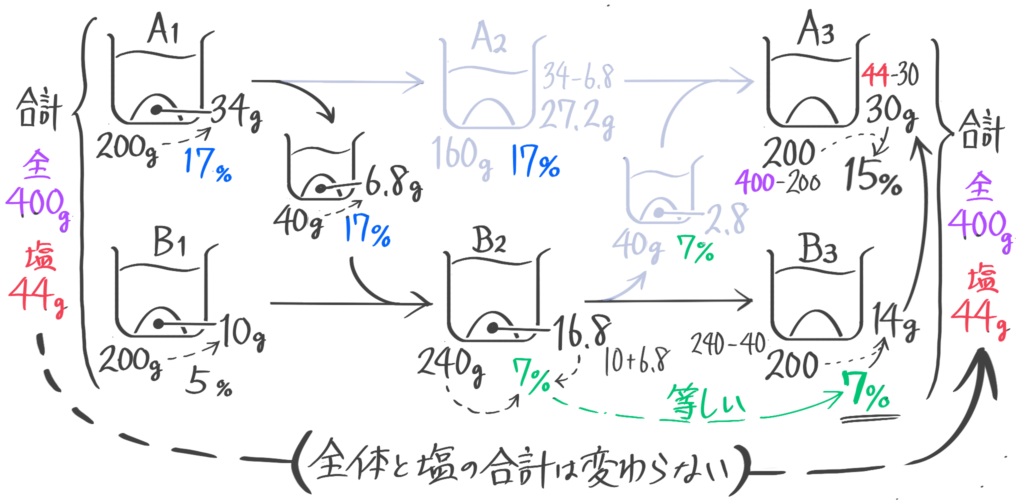
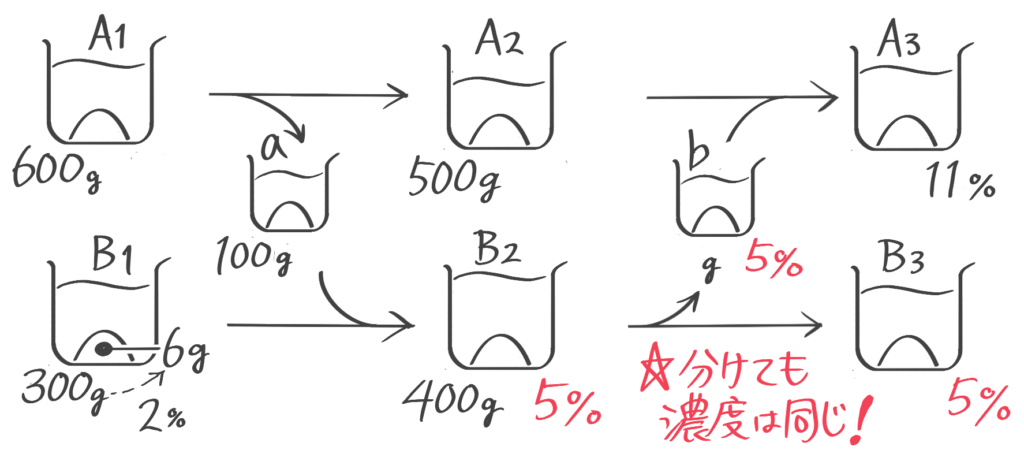
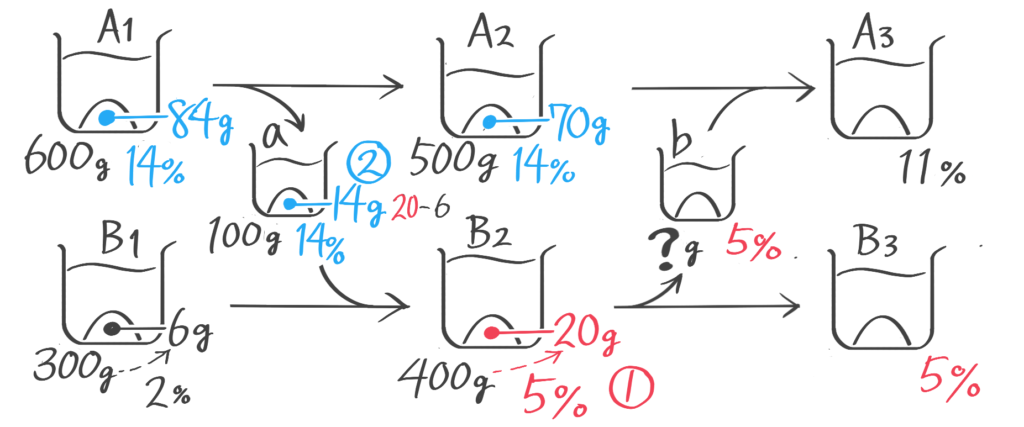
容器Aには17%の食塩水200g,Bには5%の食塩水が200gが入っている。まず容器Aから容器Bに食塩水を40g移し、次に容器Bから容器Aに40g移した。(1)容器Bの食塩水の濃さは何%になったか(2)容器Aの食塩水の濃さは何%になったか、(問題省略。テキストを見て下さい)
ビーカー図をサッと書いて状況を確認。
最初の状態(A1,B1)の塩を計算すると、AとBの合計は全体400g,塩44gと分かる
また、等しい量をやり取りするので、AもBも最後は最初と変わらず200gになります。
まず、Aから分けた40gのaとBを混合してできるB2は全体240塩16.8から濃度=16.8240x100=7%と分かります。
その後、小分けして残ったB3の濃度も7%なので塩が14gと分かります。
さらに、全体の合計400gと塩の合計44gからAの最後(A3)の全体200g,塩30gと分かるので濃度も15%と計算できる
(解答の全体像)
Aの途中A2やBから分けたビーカーは全く使わずに解けたのが分かります。
応用やり取り
ビーカー図プラス応用図(「面積図」か「てんびん図」)を使って解くもの
[例題7′]
次は面倒くさいです
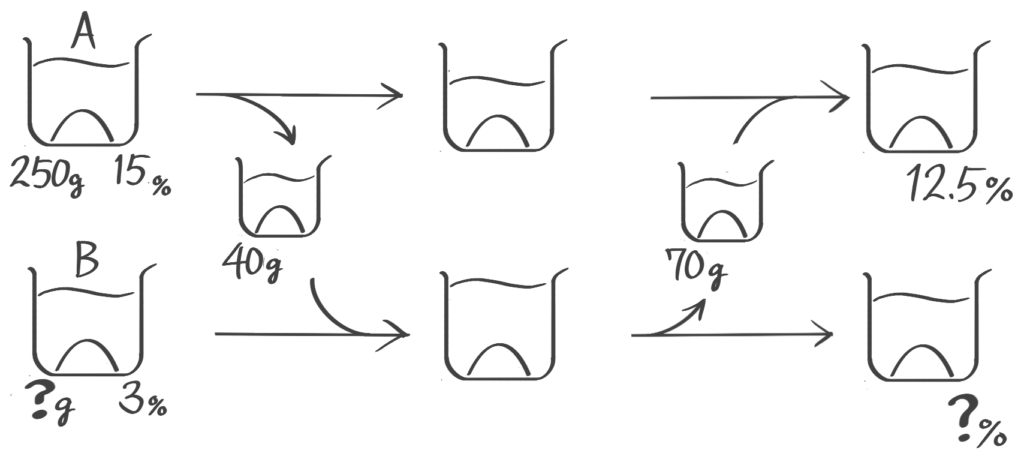
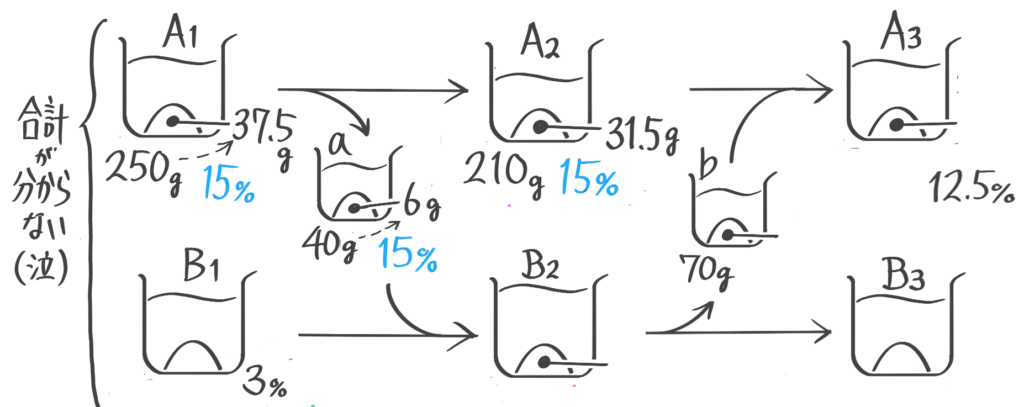
容器Aには15%の食塩水250g,Bには3%の食塩水が何gか入っている。まず容器AからBに40g移し、次に容器BからAに70g移したところ、Aの食塩水の濃さは12.5%になった。(1)容器Bの食塩水の濃さは何%になったか(2)はじめ容器Bには食塩水が何g入っていたか(問題省略。テキストを見て下さい)
ビーカー図を書き「やり取り」と判断する
まず三公式で出せるような数値を全部出してしまう
ビーカー図の限界になったので、A2とbを混合してA3を作る部分で面積図を作ってbの濃度を5%と求める(これはB2,B3の濃度でもある)
さらにaとB1を混合してB2を作る部分でも面積図を使ってB1の重さを200gと求めます
次も難しめ
(第10回 p113)
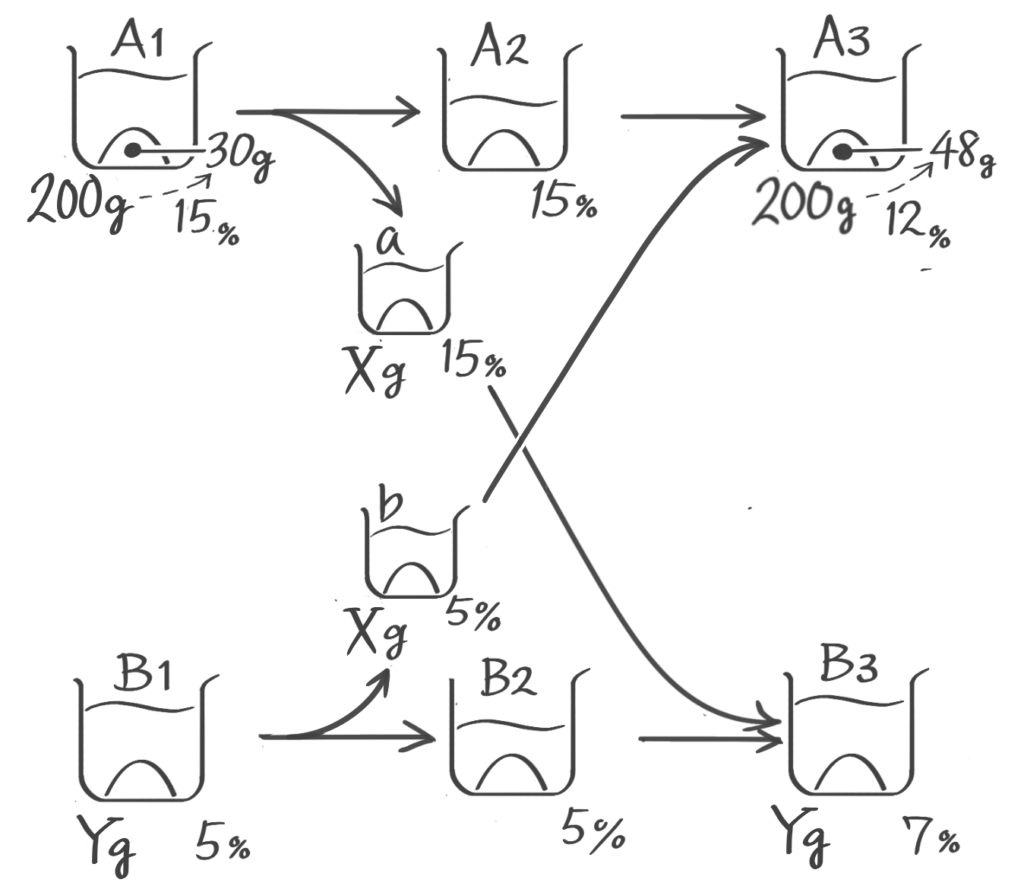
容器Aには濃さが分からない食塩水が600g,Bには2%の食塩水が300g入っている。まずAからBに100g移し、次にBからAに何gか移したところ、容器Aの食塩水の濃さは11%,容器Bの食塩水の濃さは5%になった(1)はじめ容器Aに入っていた食塩水の濃さは何％か(2)容器BからAに移した食塩水の重さは何gか(問題は省略します。テキストを見て下さい)
計算出来ることを書き込みながら、ビーカー図を書きます。
ポイントは、分けても濃度が変わらないのでB2,b,B3の濃度は等しい(5%)ことです。
B2が5%400gなので塩の重さが20gで、aに入っている塩の重さは14gと分かるので、a,A1,A2の濃度が14%と分かります。
そこで14%500gのA2と5%のbを混合して11%のA3を作る作業を面積図にしてみます
はみ出た部分が等しいことを利用してbの重さが250gと求められました♪
食塩水の交換
「やり取り」は小分けして混合、小分けして混合…を繰り返しますが、「交換」はお互いに小分けしたものを同時に混合します。
ポイントは「やり取り」と同じく
①食塩水全体の合計・塩の合計は変わらない
②食塩水を分けても濃度は変わらない
です
では、さっそく問題を解いてみましょう
基本交換
ビーカー図を丁寧に書けば解けるもの
[補完例題A]
応用交換
ビーカー図だけでは解けないもの
容器Aには15%の食塩水200g,Bには5%の食塩水が何gか入っている。2つの容器から等しい重さの食塩水を同時に取り出し、容器Aから取り出した食塩水はBへ、容器Bから取り出した食塩水はAへ移したところ、Aの食塩水は12%,Bの食塩水は7%になった。(1)容器Aから取り出した食塩水は何gか(2)始め容器Bには食塩水が何g入っていたか(問題省略。テキストを見て下さい)
問題を読みながらビーカー図を書くと「やり取り」ではなく「交換」と分かります。各ビーカーに名前をつけておきます
この問題では2つの混合が両方とも「応用混合」なので面積図を2セット書いて求めます(面倒くさい！)
まずA2とbを混合してA3を作る作業を面積図にすると
bの重さ(X)が60gと分かります。
これも使って、aとB2を混ぜてB3を作る作業を面積図にすると
B3の重さ(Y)が300gと分かります
作業の全体像はこうでした(面倒くさかった!!!)
ご案内
プリント販売(予定)
この記事で扱った基本問題・練習問題の図解プリントを記事公開期間のみの特別価格で販売しています。「教材販売所」の「ヨリシス」を御覧ください。
オンライン授業
ほぼ毎週「予習シリーズ5年」のカリキュラムに沿ったオンラインのスポット授業の生徒さんを募集しています。
無料体験は実施しませんが、初めての方は「ネタ割引」をご使用いただくと野口英世1枚程度で受講が可能です。
1回だけ短時間でも受講可能です。2回目の方は「クーポン」で安く受講が可能です
詳しくは「『そうちゃ式 家庭教師』オンライン授業」を御覧ください
終わりに
爽茶この記事を活用して成績アップを図り、志望校合格へ一歩でも近づくことを祈ります。
焦らず頑張って下さい。応援しています！
