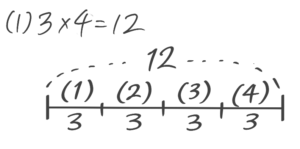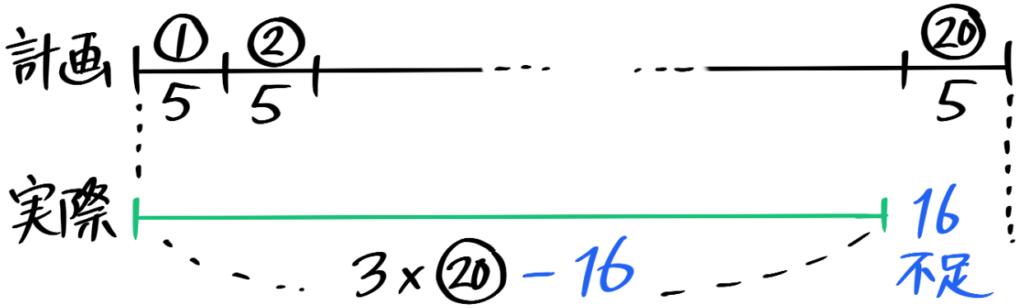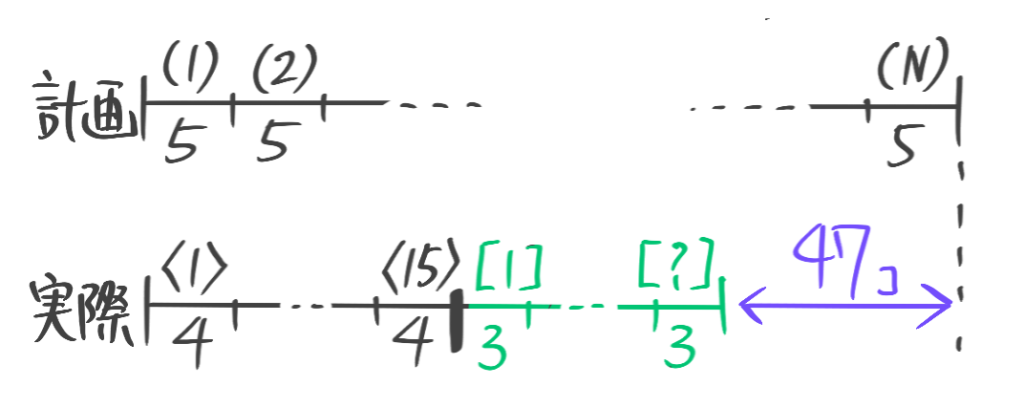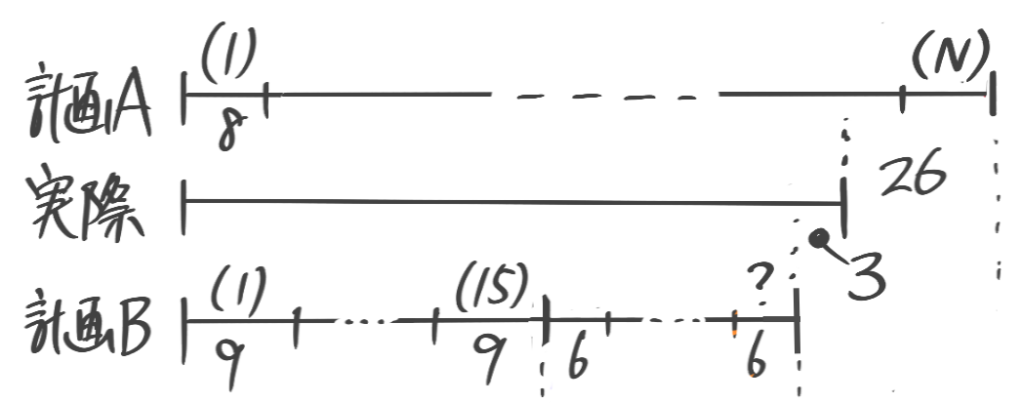「予習シリーズ」を使っている小5の中学受験生の方へ
この記事では東大卒講師歴20年超の図解講師「そうちゃ」が予習シリーズ5年(上)の第4回「いろいろな差集め算」を分かりやすく図解します
初めから読んで理解するのも良し、分からない問題の図解だけを見ても良し、自由に使って実力アップに役立てて下さい！
はじめに(ヨリシスについて)
ヨリシス by そうちゃ式
講師歴25年の図解講師「そうちゃ」が、予習シリーズ(が理解させようとしている学習体系)をスルッと理解できる「ヨリシス (Yo-Resys) by そうちゃ式」を始めます♪
予習シリーズベースで学習している小学5年生で「算数が難しい！」テキストが良くわからない…」と悩んでいる方へそれ、当然の悩みです。予習シリーズは分かりやすいテキストなのですが、4年の途中からだんだん難しくなり5年になると4年内容が前提となるので、1回分の内容は4年の最初と比べると3倍くらい！(マジで)
本来「4年内容の復習→5年内容の導入→定理公式の使い方→例題→標準問題→応用問題」という順番で学習するのが望ましいのに、授業がいきなり例題や標準問題からはじまってしまうと算数が苦手な生徒さんは「ぜんぜん分からない！」となってしまいます(涙)
もちろん、予習シリーズには「復習パート」があるのですが、その量が十分でなく、また例題なしの「いきなり標準問題」や標準問題なしの「いきなり応用問題」もあって、算数が苦手な生徒さんが「予習シリーズ」本体を十分に時間をとって予習しても完全に理解するのは難しいです。
じゃあどうすればいいの…と思ったあなた、お任せ下さい
「ヨリシス」について
「ヨリシス by そうちゃ式」は、算数が苦手な人でも理解しやすいように「予習シリーズ」の中身を並べ替えて(再体系化=リシス)そうちゃの図解を加え、さらに例題・問題の前後や途中に前提となる事柄や4年の復習を「補完例題」「補完問題」として追加したものです
算数が苦手な人でも、つまづいた例題・基本問題・練習問題の前にある「補完問題」を学習すれば、つまづきが解消して練習問題も解けるようになるでしょう。
「ヨリシス」の見方
例題,基本問題,練習問題
→「予習シリーズ」掲載の問題
番号に「’」がついているもの(ダッシュ版)は改題/自作バージョン
ダッシュ版には問題とそうちゃ式の図解がついていますが、ダッシュなしの原本版は著作権保護のため問題文は非掲載で図解のみです。
(例題はできるだけダッシュ版にして問題を掲載しています)
補完例題,補完問題→予習シリーズの例題や問題だけでは理解が難しい場合に、前提事項を基本解法を補うために追加したものです。
分からない問題の前に「補完」がある場合は、まずそちらを読むと良いでしょう♪
学習ガイド
テキストの補習に
各回のはじめに例題(類題)・基本問題・練習問題へのリンクである「問題目次」があります。
テキストを学習していて分からない例題・基本問題・練習問題がはっきりしている場合は、各回最初にある「問題目次」からそうちゃ式の「図解」へとジャンプして下さい
算数が苦手でない人は図解を見て理解できたら、ノートまたは「そうちゃ式ワーク(予リシス)」で自分でも書けるか試せば良いでしょう。
算数が苦手な人は、いきなり図解を見るよりは、その前にある「補完問題」を十分に理解(復習)して、それから図解を学習しましょう。「補完問題」も分からない場合は「そうちゃ式1号館/2号館」の該当記事へジャンプして学習して下さい。
テキストの予習に
算数が苦手な生徒さんは4年の範囲を完全に忘れていることが珍しくありません。授業の前に「ヨリシス by そうちゃ式」で各例題の前にある「補完問題」を解けるようにしておくと4年範囲が復習できて授業が分かりやすくなるでしょう。
テキストの代わりに
塾なしで予習シリーズをベースに学習していて、算数が苦手な人は予習シリーズの代わりに「ヨリシス by そうちゃ式」で学習しても良いでしょう
また講習期間などにテキストを予習・復習したい人も予習シリーズ本体よりも「ヨリシス by そうちゃ式」のほうが学習しやすいと思います。
「ヨリシス」総目次(リンク)
4(上)
4(下)
5(上)
1「約数と倍数」/2「面積の求め方」/3「割合」/4「差集め算(&過不足算)」/5「総合」
6「濃度」/7「売買」/8「多角形の回転/転がり」/9「円の回転/転がり」/10「総合」
11「並べ方」/12「組み合わせ方」/13「速さとグラフ」/14「水量変化」/15「総合」
16「旅人算とグラフ」/17「色々な旅人算」/18「数列と数表」/19「点の移動」/20「総合」
5(下)
今回の学び方
今回は「差集め算(A)」と「過不足算(B)」の大きな内容を含んでいて、テキストはAとBがゴッチャに並んでいるので、差集め(標準まで)→過不足(標準まで)→応用の順に再体系化(リシス:resystemize)しました
テキスト問題へのリンク
テキストで分からない問題がハッキリしている人は、こちらのリンクから解説を御覧ください。
(著作権を考慮し表現を変えてあります)
本回(4)
◆例題[1//2(1)/(2)/(3)//3//4//5//6//7]
◆基本問題[1(1)/(2)/(3)/(4)/(5)/(6)/(7)/(8)
2//3//4]
==================
総合回(5)
算数が苦手な人/解説がよく分からない人は、リンク先から少し上にある前提になる問題を見ると確かな理解ができるでしょう♪
差集め算
差集め算の基本
かけ算の線分図
→区切りをつなげた線分図(区切線分図)を書けるようにする
次の式を線分図にしなさい
(1)「3×4=12」
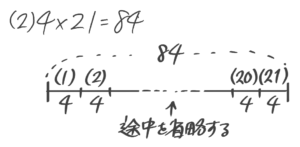
(2)「4×21=84」
★かけ算の線分図
①同じ長さ(かけられる数=3)の区切りを横につなげる
②番目を(1)から(かける数=4)まで書く
★区切りが多い場合は途中を省略してはじめ(1)と最後(かける数)の番目を書く
差集め算の基本図
→差集め算の基本図(2本の区切り線分図の(N)の右端同士を比べる)ことを覚える
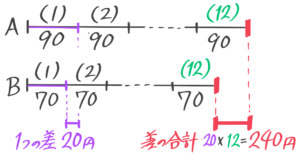
Aさんは1個90円のリンゴをBさんは70円のミカンをそれぞれ12個ずつ買うと2人の払った代金の差がいくらになるか、1個ずつの差から求めて線分図に示せ
★同じ番目の区切り(ここでは12)の右端を太くして、その差(幅)が差の合計になる。差集め算はこの図がすべての出発点になる
払った代金の差=差の合計=20×12=240円
差集め算の基本問題
→基本図を使って問いに答える
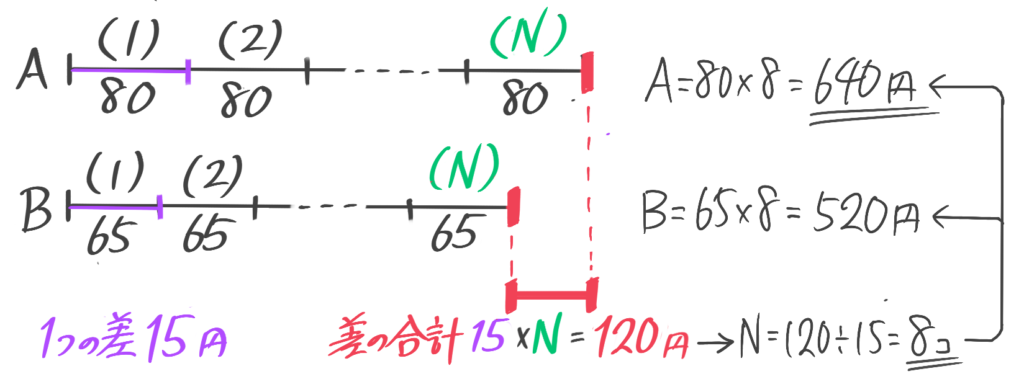
Aさんは1個80円のリンゴを、Bさんは65円のミカンを同じ数ずつ買ったところ、2人の払った代金の差は120円だった。
(1)何個ずつ買ったか
(2)Aさんが払った代金は何円か
★個数が分からないときは(N)として区切り線分図を書く
リンゴとミカンの単価の差15円が(N)個あつまって代金の差120円になるので、15xN=120を逆算してN=120÷15=8。
また、Aが払った代金は80×8(N)=640円
[基本問題1(1)]
(↑例題1’を参照して下さい)
[基本問題1(2)]
(↑例題1’を参照して下さい)
[基本問題1(3)]
(↑例題1’を参照して下さい)
[基本問題1(4)]
(↑例題1’を参照して下さい)
[5回-基本問題10(1)]
(↑例題1’を参照して下さい)
差集め算の三公式
●差の合計(40)=1個あたりの差(2)×個数(N=20)
○個数(N:20)=差の合計(40)÷1個の差(2)
○1個の差(2)=差の合計(40)÷個数(N=20)
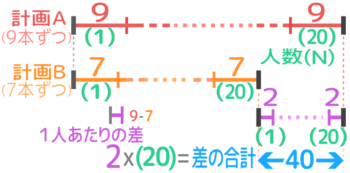
→実際は三公式のうち「差の合計=1つの差x(N:個数)」を基本図と一緒に覚えれば良い。(5年生なので1つの差とNは逆算で求められるので)
不ぞろいな差集め算
個数=Nがそろっていない場合
個数が不ぞろい時の線分図
「○個多い」の表現(「N」と「N+○」)を憶える
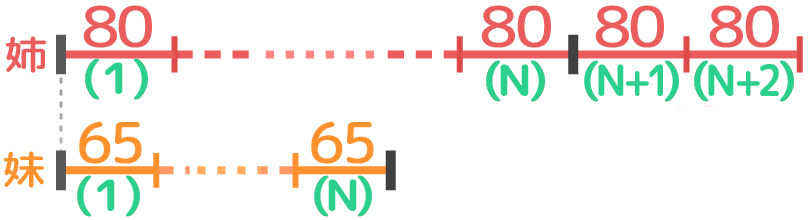
妹が1個65円のペンを何本か買い、姉は80円のペンを妹より2本多く買った。2人が払う代金をそれぞれ線分図で表わせ
★ポイント
①少ない妹の個数を(N)、姉の個数を(N+2)とする。
②姉は(N)から上(右)に区切りが2つ(N+1)(N+2)あることを表現する。
③姉妹の(N)の右端を太くする
Nを求める
不ぞろい時にも(N)同士を比べて差の合計を求めることを理解実践する
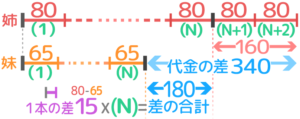
妹が1個65円のペンを何本か買い、姉は80円のペンを妹より2本多く買ったところ、姉がはらった代金は妹より340円高くなった。姉と妹はそれぞれペンを何本ずつ買ったか
★(N)の右端を比べて差の合計とNを求める
姉妹の(N)の右端の間(差の合計)は340-160=180円。
1個の差は80-65=15円なので、妹の本数(N)=180÷15=12本で、姉の本数(N+2)=12+2=14本
[基本問題3]
(↑例題3’を参照して下さい)
[基本問題4]
(↑例題3’を参照して下さい)
[5回-基本問題12]
(↑例題3’を参照して下さい)
一方の単価を求める
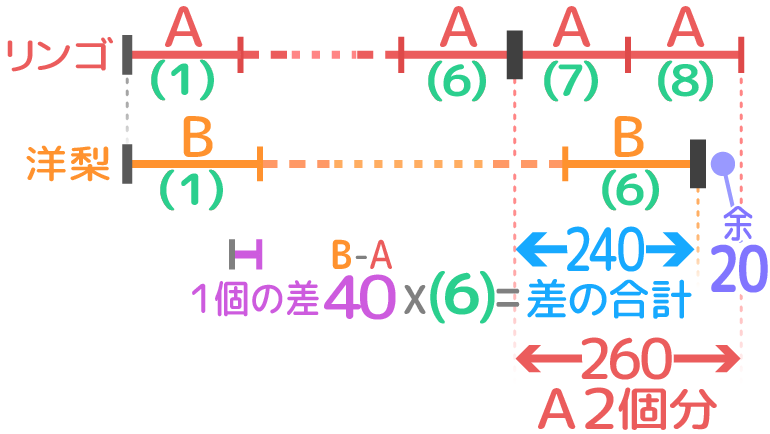
個数は問題に書いてあり、一方の単価(小さな区切りの大きさ)を求める問題。とにかく基本線分図を書いて同じ個数の区切りの右端を比べる
リンゴをちょうど8個買える金額を用意して買い物に行った、気が変わって40円高い洋梨を買うことにしたところ6個買えて20円余った。リンゴは1個何円か？
★少ないリンゴの個数(6)を両方の線分に描き、(6)の右端の区切りを比べる
(6)の区切りの間=差の合計=40x(6)=240。
余りの20円を加えた260円がリンゴ2つ分((7)と(8))なので、リンゴ1個は260÷2=130円
対応する基本問題・練習問題が見当たらないので作成準備中(2023.3.3)
共通部分を使う差集め算
計画と実際など2つの場合の全体の個数ではなく、個数の差が示される場合。例題はありません(汗)
(総合回：5回p59)
(2) (問題は省略します。予習シリーズ本体を参照して下さい)
アメがチョコより多い6個分を除いた「個数が等しい部分」をN個として差集め算の図を作ると、チョコの代金が30x(N)円多いと分かる。
そして、つなげたアメの線分とチョコを比べると、先程の差の合計30xN=120+150=270と分かる
N(チョコの個数)=270÷30=9、アメの個数=N+6=15と求められる。
つるかめ算を差集めで
予習シリーズは「つるかめ算」を差集めで学習しているので、その延長になる
参考:基本のつるかめ算
(テスト範囲外:スキップしてもOK)
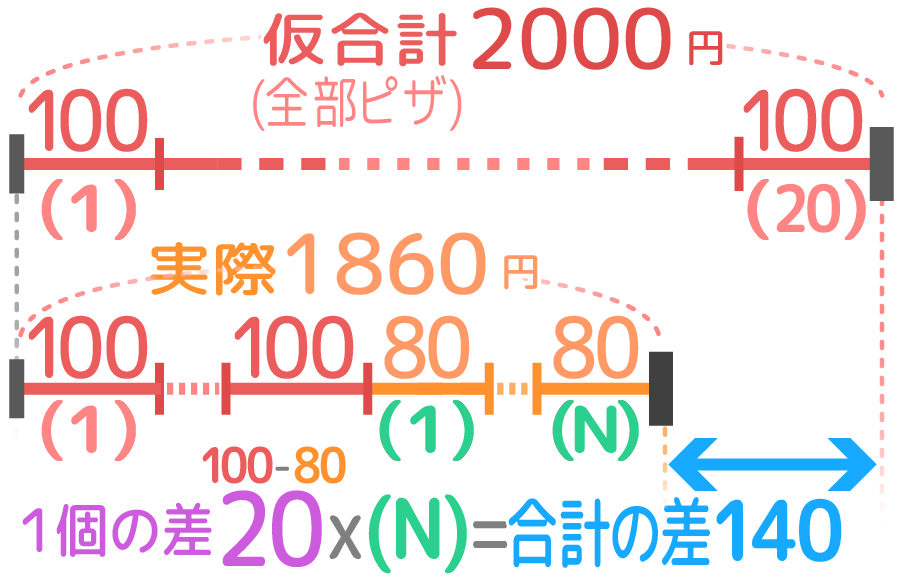
仮の合計と実際の値段を差集め算の区切り線分図にあらわして計算する
100円のピザまんと80円の肉まんを合わせて20個買ったら1860円だった。ピザまんと肉まんをそれぞれ何個買ったか
全部ピザまんだった場合の仮合計(2000)と実際の代金(1860)の合計の差=140円
これは全部ピザまんから1個を肉まんに買えた場合の差(100-80=20)がN個集まったもの
つまり肉まんの個数(N)x20=140なので、肉まんは140÷20=7個、ピザまんは20-7=13個
個数の取り違え
二種類の品目を買うときに、個数の取り違えで代金に差が生じる仕組みをまず理解する
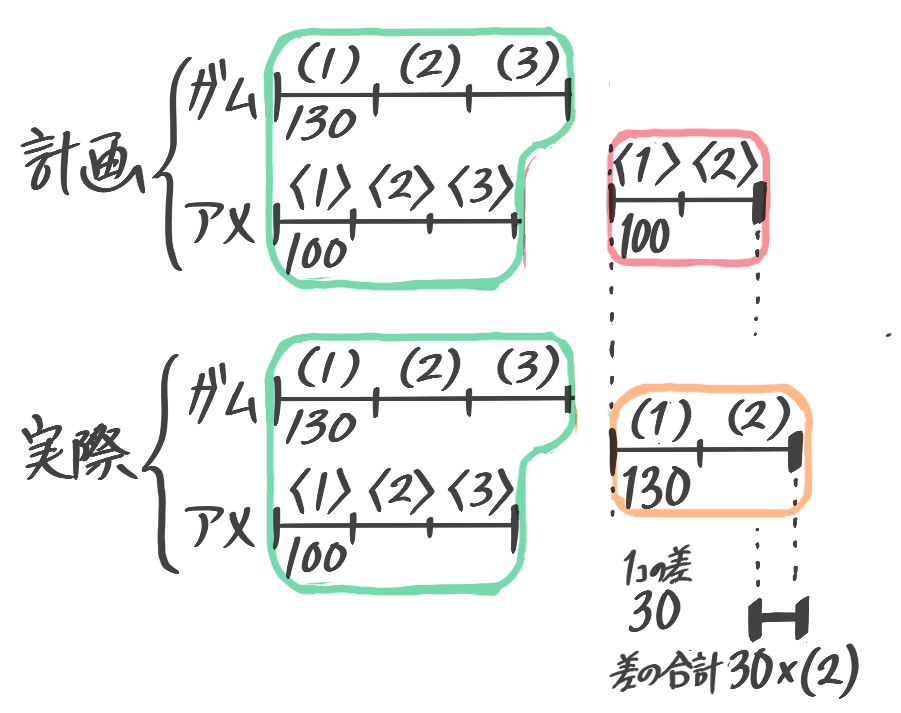
130円のアメを3個、100円のガムを5個買うつもりが、個数を逆に取り違えて買ってしまった場合の代金の差はいくらか(途中計算でかけ算は1回しか使わないこと!)
計画(アメ3ガム5)と実際(アメ5ガム3)の線分図を書いて比べると、ガムとアメ3個ずつの部分(個痛共通部分)は計画と実際で等しいのが分かる
違いが生まれるのは個数が違う部分(個数の差5-3=2個ずつの部分)で、ここで差集め算の線分図を作ってみると
1個の差(30)x個数の差(2)=差の合計60円が、計画と実際の代金の差になっているのが分かる
この「個数取り違え」の考え方は公式としても憶えておきましょう
→個数の差で「予定と実際の代金の差」が発生する
●予定と実際の代金の差=個数の差×単価の差
(例)30円アメ12個と50円のガム8個を買うつもりが
個数を逆にしてしまった場合
→個数の差(12-8)×単価の差(50-30)
=4×20=予定と実際で代金に80円の差が生じる
取り違えのつるかめ算
「個数共通部分」と「個数差の部分」考え方を利用する練習
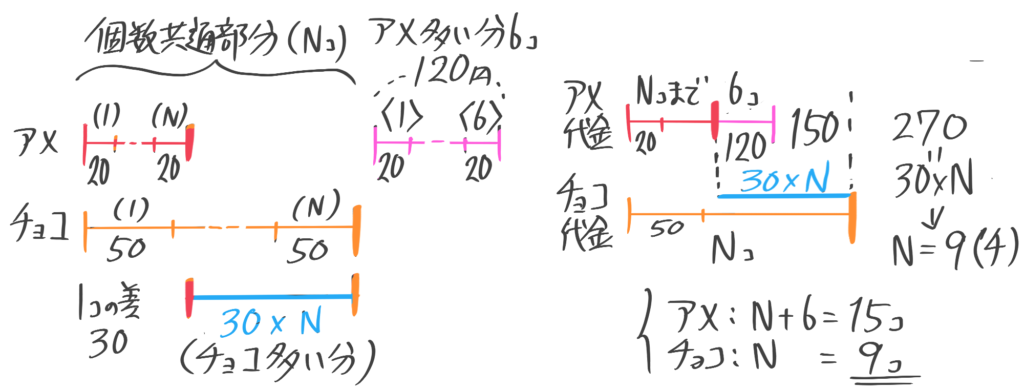
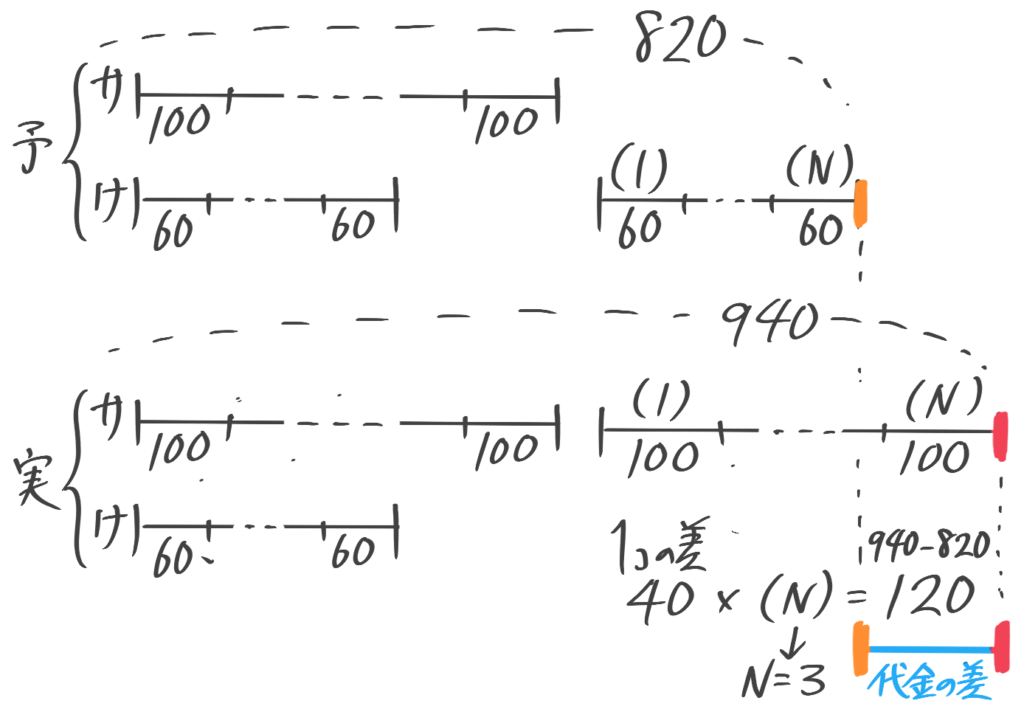
90円のピザまんと120円の肉まんを合わせて20個買う予定だったが、間違えて買う個数を逆にしてしまったので、実際の代金が予定よりも180円高くなった。予定ではピザまん・肉まんをそれぞれ何個買う予定だったか
補完例題の図を思い出して個数の差が(N)個として線分図を書く。取り違えで高くなったので、予定では安いピザまんが、実際は高い肉まんが多いと予想できる。
また、共通部分の個数は分からなくても解けるので番目を書かなくても良い
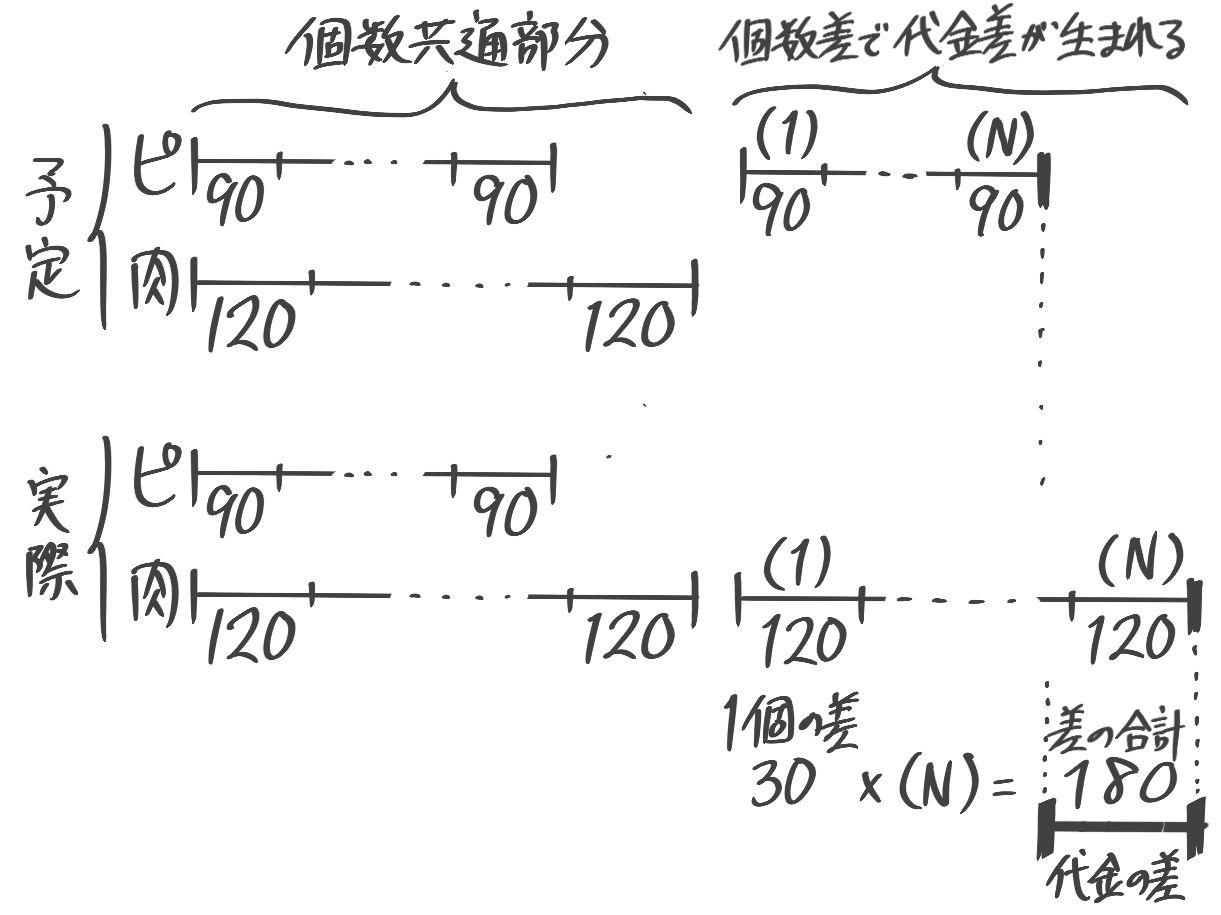
ピザまんと肉まん1個の差が30円x個数の差(N)=予定と実際の代金の差(180) なので、N=180÷30=6個と求められる。
★慣れてきたら図を書かずに公式一発でも良い
よって、予定ではピザまんと肉まん合わせて20個(問題文より)、ピザまんが6個多いと分かった
和差算を解いてピザまんは(20+6)÷2=13個、肉まんは(20-6)÷2=7個
合計金額が書いてある取り違え
合計個数でなく合計金額が書いてある場合。図は同じで、その後の計算方法が異なる
(著作権の関係で問題文は省略致します。「予習シリーズ5(上)」を参照して下さい)
「取り違え」の図を書いて、個数が違う部分を差集め算の線分図にする
N(個数の差)が3個と出たら、サインペンが多い部分=100×3=300円なので、残りの個数共通部分=940-300=640円と分かる
サインペン100円と蛍光ペン60円のペア160円が個数共通部分640の中に640÷160=4個あるので、サインペンは全部で4+3=7本、蛍光ペンは4本
(総合回：5回p)
(3) 問題は省略。予習シリーズ本体を参照して下さい
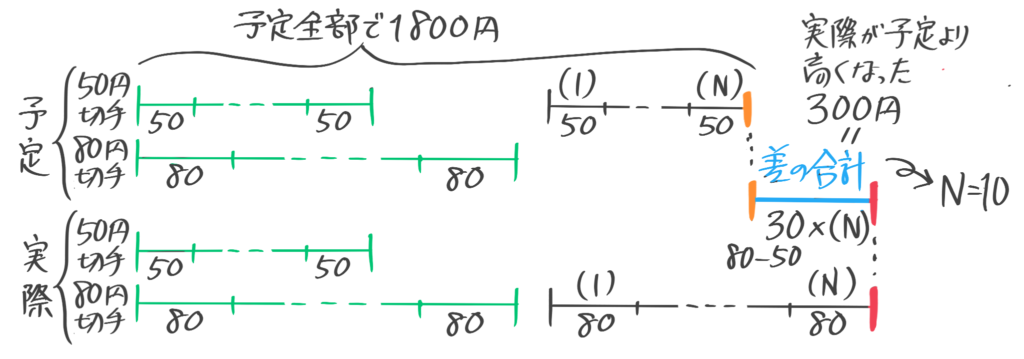
取り違えて高くなったので、予定は安い50円切手を多く買い、実際は80円切手を多く買う線分図を作る。予定の金額が書いてあるのがこの問題の特徴
個数の差の部分で差集め算を作ると、差の合計(予定より高くなった300円)=1枚の価格差(80-50)x枚数差(N)より、N=300÷30=10枚。
予定のうち、個数の差(10個)部分の50円切手の代金は50×10=500円なので、残りの「個数共通部分」の値段は1800-500=1300円。50円切手と80円切手1枚づつをペア130円にすると、1300÷130=10ペア出来るので共通部分はそれぞれ10枚
よって50円切手は共通部分10枚+差の部分10枚=20枚、80円切手は共通部分の10枚と分かりました。
分かりましたか？
これでいわゆる「差集め算」は終了です。次は差集め算の発展形「過不足算」です。
過不足算
過不足算は差集め算の応用です(「そうちゃ式」では、2本の線分図で解くのを「差集め算」3本の線分図で解くのを「過不足算」としています。)
過不足算の準備
余りと不足の表現
「計画」と「実際」二本の線分図の長短をイメージできるようにする
以下の問いに線分図を書いて答えなさい
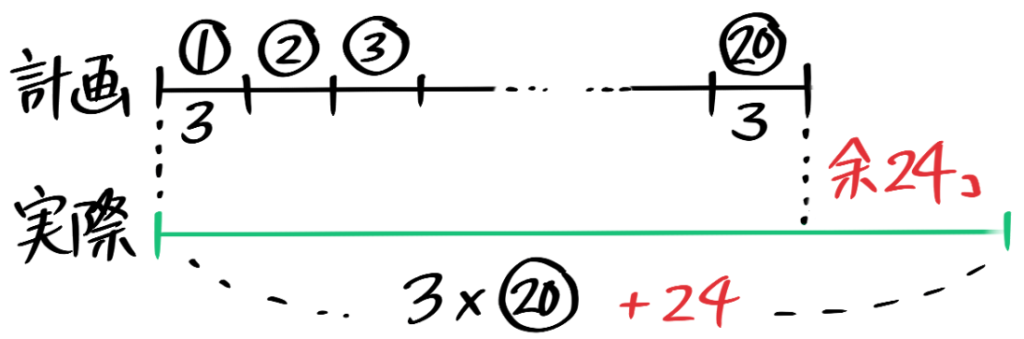
(1)20人の生徒にアメを3個づつ配ろうとしたら24個余った。アメは実際に何個あるか？線分図でも表わせ
(2)20人の生徒にアメを5個づつ配ろうとしたら16個足りなかった。アメは実際に何個あるか？線分図でも表わせ
「余り」→「計画(配ろうとする本数)」の線分図が「実際の本数」の線分図よりも短くなる
実際=3×20+24=84個
「不足」→「計画」の線分図が「実際」の線分図よりも長くなる
実際=5×20-16=84個
過不足算の基本図
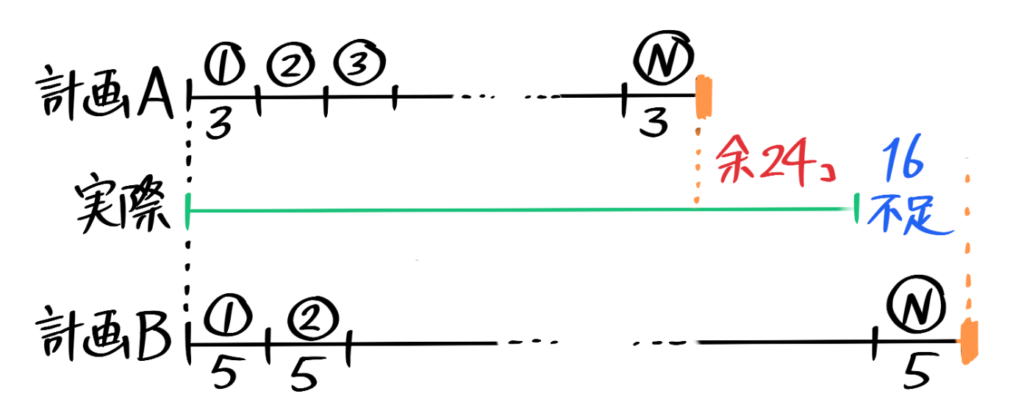
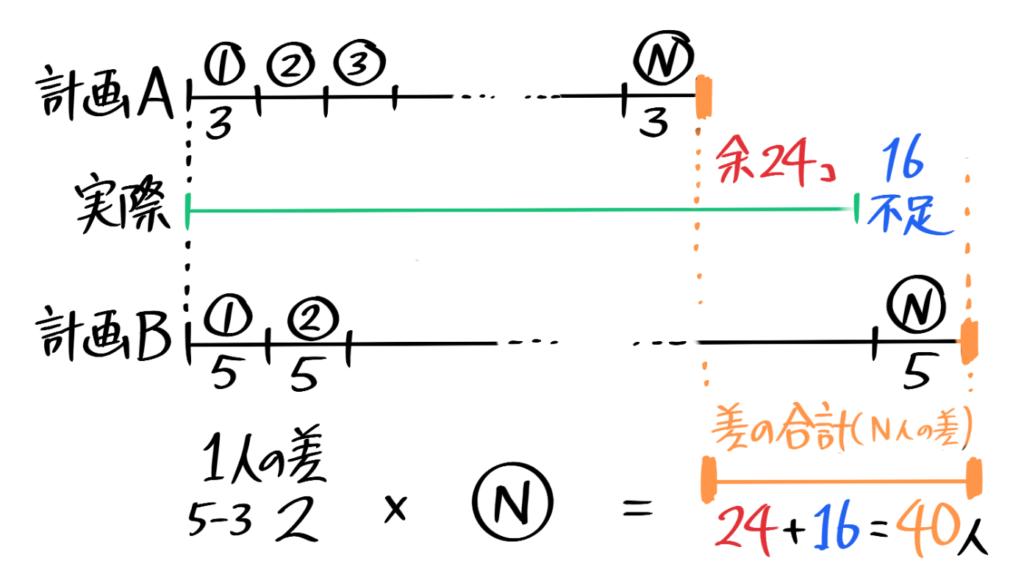
2つの「計画」の間に「実際」の計3本の線分図を書く練習をする(差集め算は2本の線分図を比べたが、過不足算では3本を比べる)
60個のアメを生徒に分ける。3個づつ配ろう(計画A)としたら24個余り、5個づつ配ろう(計画B)としたら16個足りなかった。計画Aと計画Bで必要な本数の差は何本か(線分図を書いて求めなさい)
生徒の人数が分からないので(N)人として、3個ずつ配る計画Aと5個ずつ配る計画Bの間に「実際」の線分図を書く
計画Aは実際より24短く(余り)、Bは実際より16長い(不足)
2つの計画の差は24+16=40と分かります。
これは計画AとBの2つの(N)の間の大きさ(「差の合計」)なので
N=40÷2=20人と分かります
これで過不足算を解く準備ができました♪
過不足算の基本3パターン
三本の線分図から差の合計を読み取ってNを求めてから実際の本数を求める、という手順を身につける
「余って足りない」
用意した折り紙を何人かの子供に配る。1人に3枚ずつ配ると24枚余るが、5枚ずつ配るには16枚足りない。子供の人数と折り紙の枚数を求めよ
生徒の人数が分からないので(N)人として、3個ずつ配る計画Aと5個ずつ配る計画Bの間に「実際」の線分図を書く(上の補完例題2-2と同じ図)
計画Aは実際より24短く(余り)、Bは実際より16長い(不足)
計画AとBの2つの(N)の区切りの右端の間=「差の合計」=40なので、1人の差(2)x人数(N)=40 よりN=40÷2=20人
実際の数は3×20+24=84枚(Aから求める)または5×20-16=84枚(Bから求める)
[基本問題1(6)]
(↑例題2′(1)を参照して下さい)
[5回-基本問題10(3)]
(↑例題2′(1)を参照して下さい)
「まだ余る」
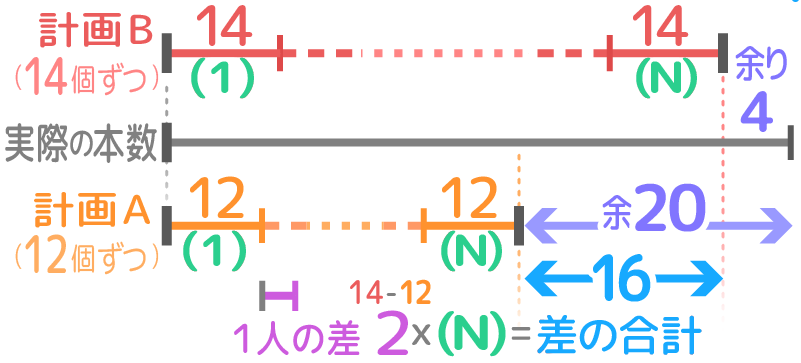
用意したアメを何人かの子供に配る。1人に12個ずつ配ると16個余り、14個ずつ配ってもまだ4個余る。子供の人数とアメの個数を求めよ
計画Aも計画Bも「余る」ので実際の個数より短くなるのに注意して線分図を書く
AとBの(N)の区切りの右端の間=差の合計は20-4=16なので、一人の差(2)x人数(N)=16よりN=16÷2=8人。
実際の個数は12×8+20(Aから)または14×8+4(Bから)=116個と分かります。
イスに座る問題では「座れない」が何を意味するのか注意して下さい
次の問いに答えなさい
(7) (問題は省略します。「予習シリーズ」を参照して下さい)
★イスに座れない=イスが「足りない」ではなく、人数が「余る」というのを理解する
1脚の差(3)x椅子の数(N)=差の合計(27)より、N=27÷3=9脚。生徒数は7×9+29=92人
[基本問題1(8)]
(↑例題2′(2)を参照して下さい)
「まだ足りない」
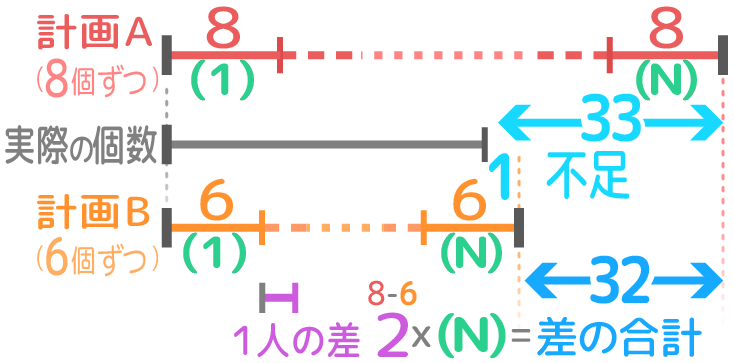
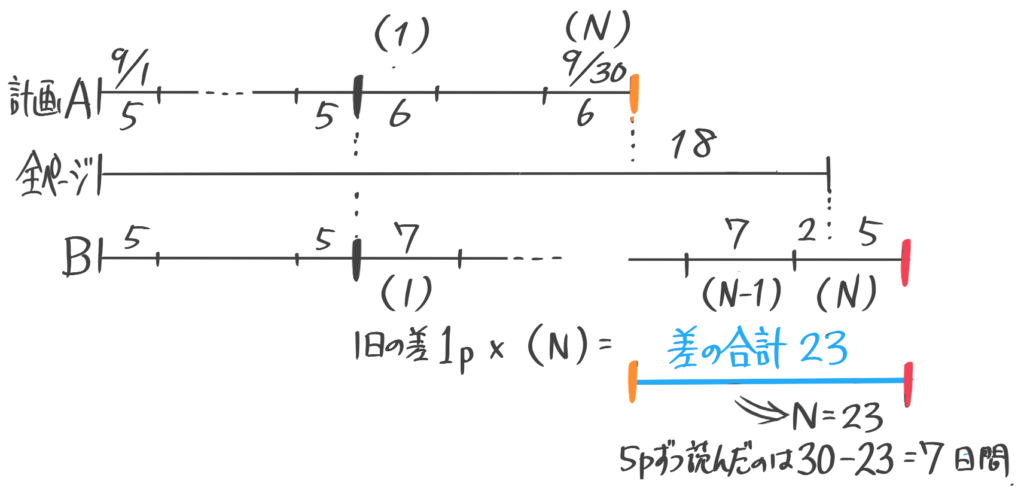
用意した鉛筆を何人かの子供に配る。1人に8本ずつ配ると33本足りず、6本ずつ配ってもまだ1本足りない。子供の人数と鉛筆の本数を求めよ
「計画A(通りに配るのに必要な個数)」「計画B(通りに配るのに必要な個数)」ともに「足りない」ので、2つの計画の線分図はともに「実際」より長くなる。
AとBの(N)の区切りの右端の間=差の合計は33-1=32なので、一人の差(2)x人数(N)=32よりN=32÷2=16人。
実際の個数は8×16-33(Aから)または6×16-1(Bから)=95本と分かります。
[基本問題1(5)]
(↑例題2′(3)を参照して下さい)
[5回-基本問題10(4)]
(↑例題2′(3)を参照して下さい)
不ぞろいの過不足算
線分を3本書く場合は過不足とします。
[補完例題C]
(2023.3.5計画中)
Nを求める
買い物に行ったAさんは1本150円のジュースを何本か買って100円余る予定だったが、1本が120円になっていたので予定よりも2本多く変えて40円余った。実際に買った個数とはじめの所持金を求めなさい
予定の線分は150円の区切りをN個つなげて所持金より100円少なく、実際の線分は120円の区切りを(N+2)個つなげて所持金より40円少ない
(N)の右端同士を比べると差の合計は180円,1個の差は30円なので、N=180÷30=6個。
所持金は150×6+100(予定から)または120×8+40(実際から)=1000円と分かります。
[5回-基本問題10(2)]
(↑例題4’を参照して下さい)
単価を求める
(問題は省略します。予習シリーズ本体を参照して下さい)
線分図を書いて(16)の右端を比べる
(1)16本買ったときの差の合計が320円で、そのときの余りは、ボールペンを買った余り60円を加えた380円
(2)鉛筆5本分=350円から鉛筆1本=70円と分かるので、所持金は70×21+30=1500円と求められる
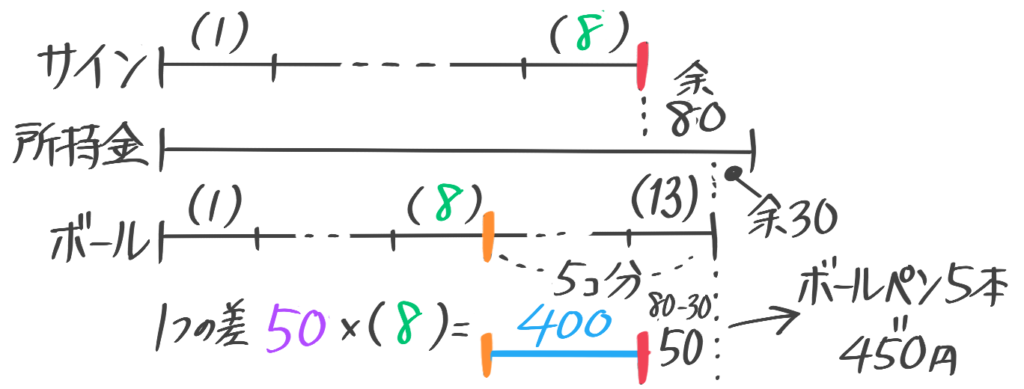
Aさんが持っているお金でサインペンを買うと8本買えて80円あまり、ボールペンを買うと13本買えて30円あまる。サインペン1本がボールペンより50円高い。
(1)サインペンとボールペンはそれぞれいくらか
(2)Aさんの所持金はいくらか
問題文を線分図にして、(8)の右端を比べると差の合計=50×8=400円、ボールペン5本分=450円と分かる
ボールペン1本=450÷5=90円で、サインペン1本=90+50=140円
所持金は90×13+30(ボールペンから)または140×8+80(サインペンから)=1200円と分かります
端数の過不足算
この項目は例題がなく、いきなり基本問題が出てくる
端数を表す線分図
決まった量(1人「5」個ずつ配る、1脚に「5」人ずつ座る)に満たないもの(「3」個しかもらえない人、「3」人しか座らないイス)がある場合の線分図の表現
線分図を書いて求めなさい
(1)生徒にアメを6個づつ配ったところ、1人の生徒は4個しかもらえず、まったくもらえない生徒も1人いた。アメは何個不足しているか
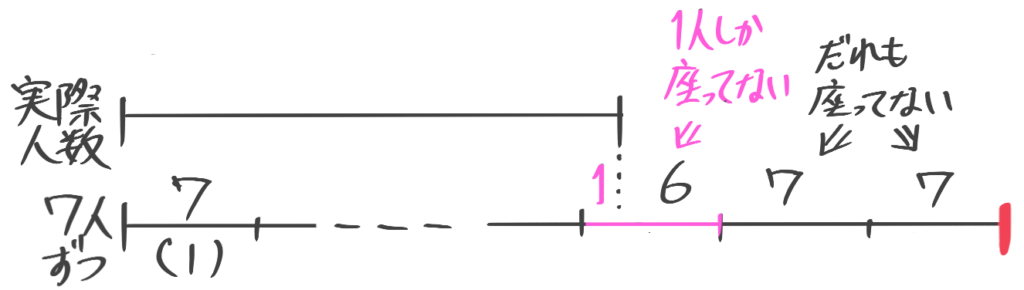
(2)子供たちを長イスに7人ずつ座らせたところ、1人しか座らないイスが1つと誰も座らないイスが2つできた。あと何人座れるか
「計画」の線分を基準に「実際の個数」の線分の長さを考えると、「計画」の最後から2人目の途中まで(4人)の長さになる。
不足しているのは、最後から2人目のあと2個と最後の1人の6個を合わせた8個と分かる
「計画(7人ずつ座らせたときに全部で座れる人数)」の線分を基準に「実際の人数」の線分の長さを考えると、「計画」の最後から3脚目の途中まで(1人)の長さになる。
あと座れるのは、最後から3脚目のあと6人と最後の2脚の7×2=14人を合わせた20人と分かる
端数の過不足算の解法
端数の線分図で(N)同士の右端の幅を見つける
線分図を書いて答えなさい
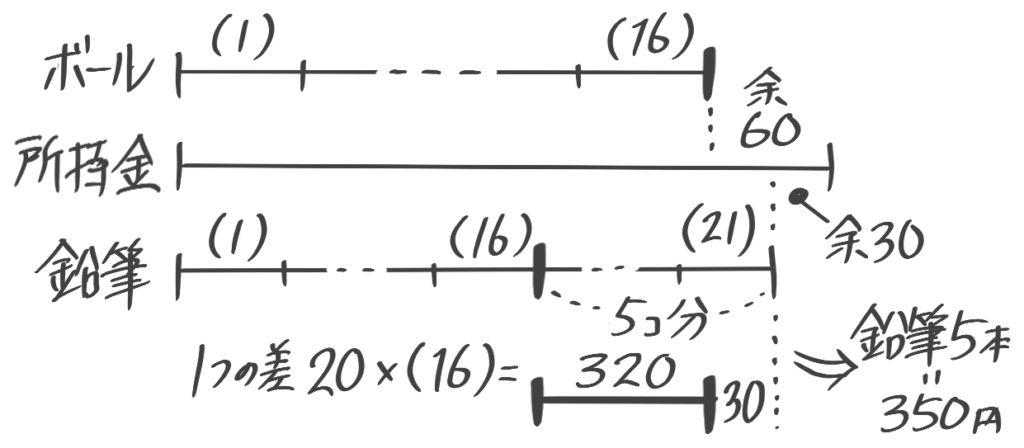
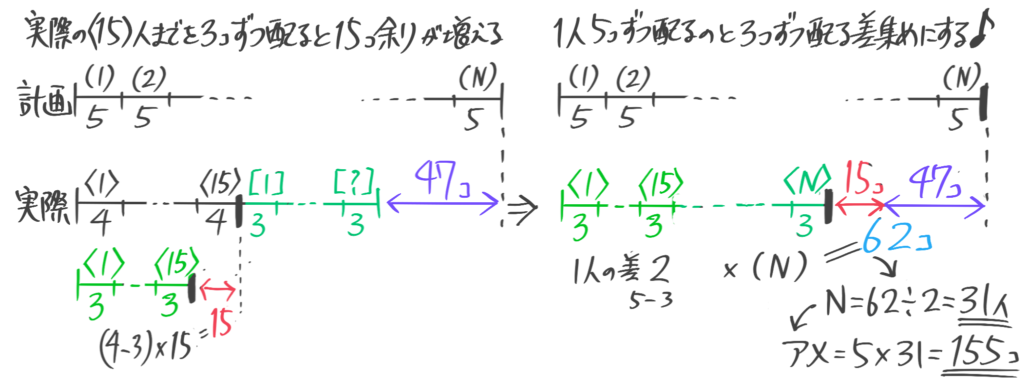
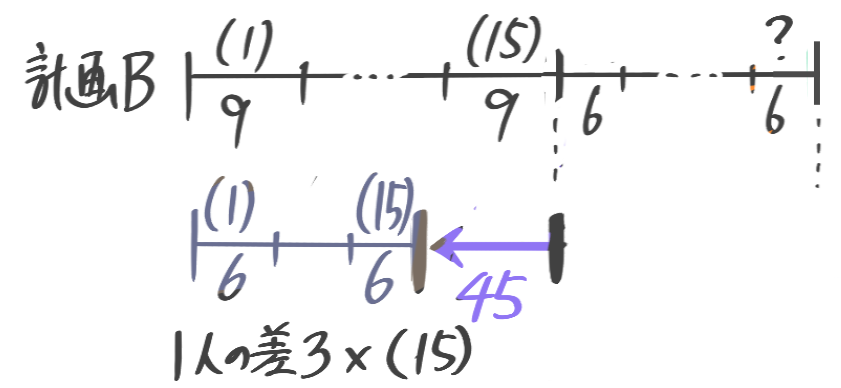
(1)何人かの生徒にアメを5個ずつ配ったところ13個余ったので、今度は6個ずつ配り直したところ1人の生徒は4個しかもらえず、まったくもらえない生徒も1人いた。生徒の人数とアメの個数を求めよ
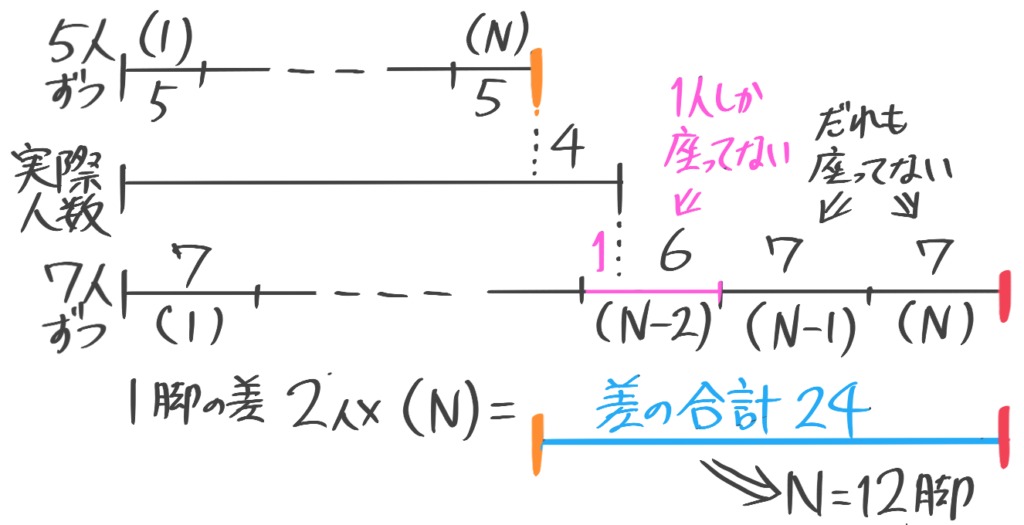
(2)子供たちを長イスに5人ずつ座らせたところ、4人座れなかったので、今度は7人ずつ座らせたところ、1人しか座らないイスが1つと誰も座らないイスが2つできた。子供の人数とイスの数を求めよ
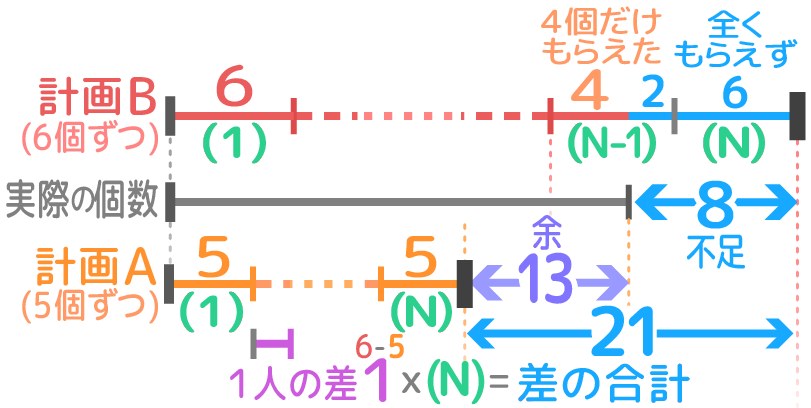
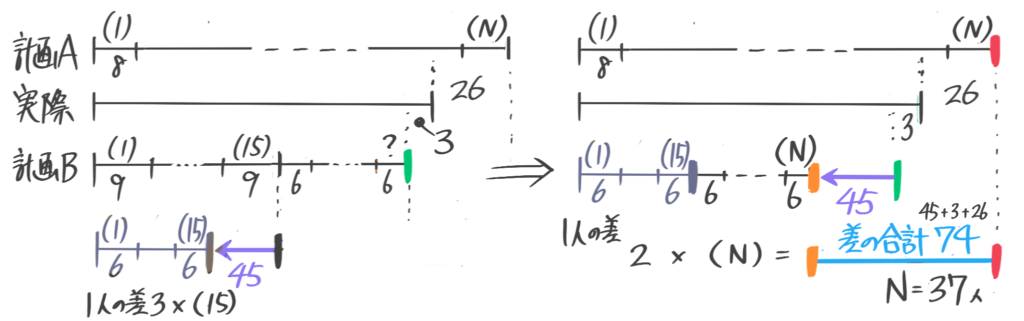
実際の個数を真ん中にして、計画AとBの線分図を上下に書く
計画AとBの(N)の区切りの右端の間=差の合計=13+8=21なので、1人の差(1)x(N)=21よりN=21人
実際の個数=5×21+13=118個と分かります
子供の人数を真ん中にして、計画AとBの線分図を上下に書く
計画AとBの(N)の区切りの右端の間=差の合計は5人ずつのときの余り4+7人ずつのときのあと座れる人数6+7+7=20人の合計24人なので、1脚の差(2)x(N)=24よりN=12脚
子供の人数=5×12+4=64人と分かります
(問題文章は省略します。予習シリーズ本体を見て下さい)
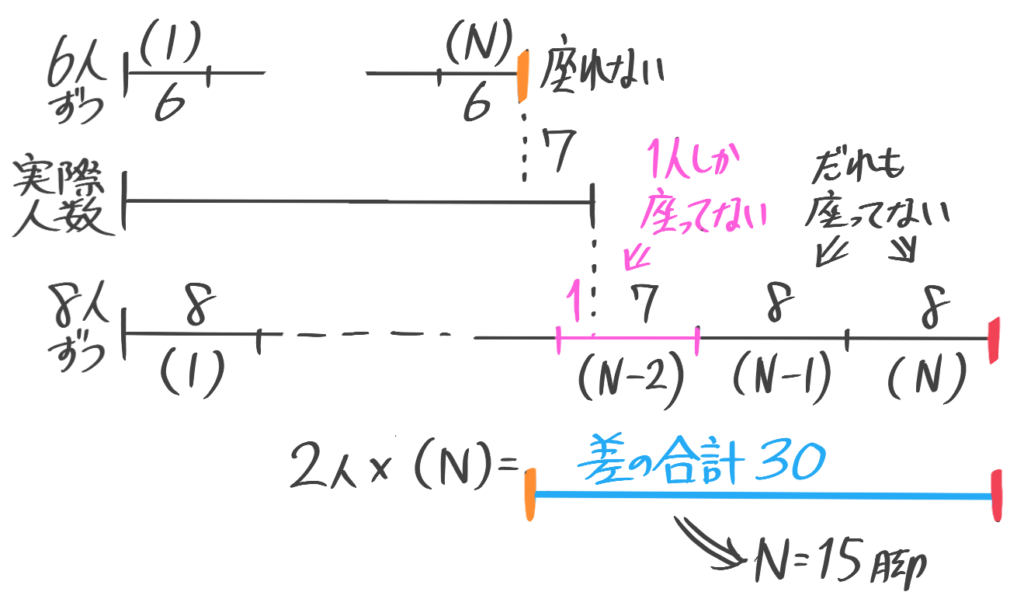
(1)1脚に8人ずつ座っていくと、空席は何人分できるか
(2)5年生は何人か
子供の人数を真ん中にして、計画A(6人がけで座れる人数)と計画B(8人がけで座れる人数)の線分図を上下に書く。
(1)8人がけでは、あと7+8+8=23人座れると分かる
(2)計画AとBの(N)の区切りの右端の間=差の合計は6人がけの座れない7人+8人がけのあと座れる人数23人の合計30人なので、1脚の差(2)x(N)=30よりN=15脚
子供の人数=6×15+7=97人と分かります
[5回-基本問題11]
(↑4回基本問題2を参照して下さい)
(問題は省略します。予習シリーズ本体を参照して下さい)
計画AとBの線分の間にページ数の線分を書くと、Bの最後の日(N)の途中までの長さ(2)になる。
(N)の右端の区切りの幅(差の合計)は18+(7-2)=23なのでN=23日間(9/8~9/30)で5pずつ読んでいたのは30-23=7日間(9/1~9/7)と分かる
これで、本のページ数=5×7+6×23+18=191pと求められる
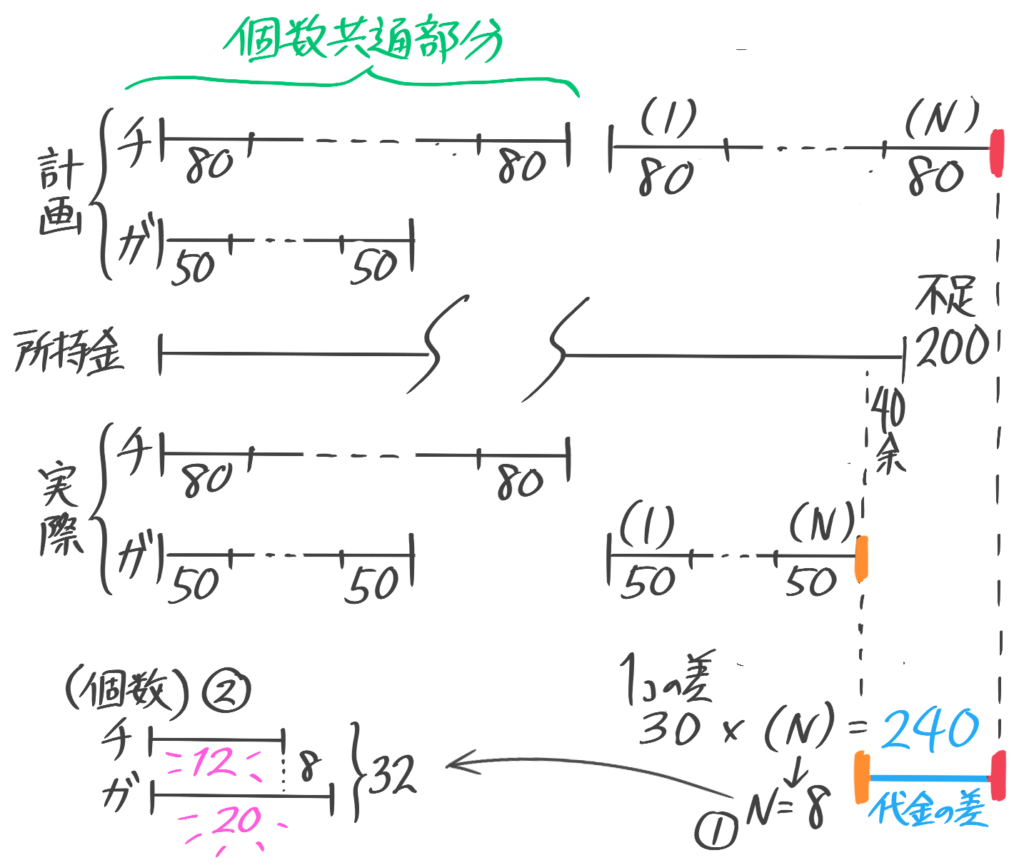
取り違えの過不足算
つるかめ取り違え(例題6)の図に「実際」の線分図を加えて3本にする
(問題文は省略します。予習シリーズ本体を参照して下さい)
(1)実際に買った個数はガムとチョコどちらが何個多いか
(2)はじめに何円持っていたか
個数を逆にしたら代金が少なくなったので、実際は安い方(ガム)が多いと分かる。
取り違えのつるかめの線分図の間に実際のお金を入れて、個数が違う部分を過不足算にする。
代金の差=200+40=240円なので、N(個数の差)=240÷30=8個
ガムとチョコの和32差8の和差算(ガムが多い)を解いてチョコ12個ガム20個
所持金は80×12+50×20+40=2000円と分かります
差集め/過不足の応用問題
ここから先は応用問題です。各タイプの補完例題→差集め算→過不足算の順に説明してあります
途中変化の問題
1人に配る個数などが途中で変わる場合。けっこう難しい(テキストに例題なし)ので苦手な人は6年以降に取り組めば良い
[補完例題B]
20223.3.4作成中
途中変化の差集め算
(総合回:5回)
(1)(問題文は省略します。予習シリーズ本体を参照して下さい)
問題文の条件をそのまま図にすると、同じ個数の区切りが並んでいないので差集め算が使えない。
そこで、実際の15人までに3個ずつ配るよう変更すると、15個余計に余りがでるが、全員に3個ずつ配ることになり、差集め算が使えるようになる。
差の合計は、もともとの余り47に4個を3個に変更したことによる15個の余りを加えた62個になるので、人数(N)=差の合計(62)÷1人の差(5-3)=31人。
アメの個数は5×31=155個になる
途中変化の過不足算
三本の線分図を利用する問題
(問題は省略します。予習シリーズ本体を参照して下さい)
(1)アメを全員に6個ずつ配ると何個あまるか
(2)アメは全部で何個あるか
(1)問題文を線分図にしても個数が共通する(N)が無い…
計画Bの(15)までを9個ずつから6個に減らすと、計画Bの線分は1人の差3x(15)=45短くなる
これを計画Bの線分の15人までと入れ替えると
全員(N)に6個配った線分ができる♪このとき実際との差=余りは45+3=48個
(2)また、2つの(N)の右端の幅=差の合計=74なので、2xN=74よりN=37人
アメの個数は6×37+48=270個
ペアを作る問題
テキストでは一番難しい問題が例題になっていて！学びづらい
ペアの線分図
「ペアの線分図」を理解実践する
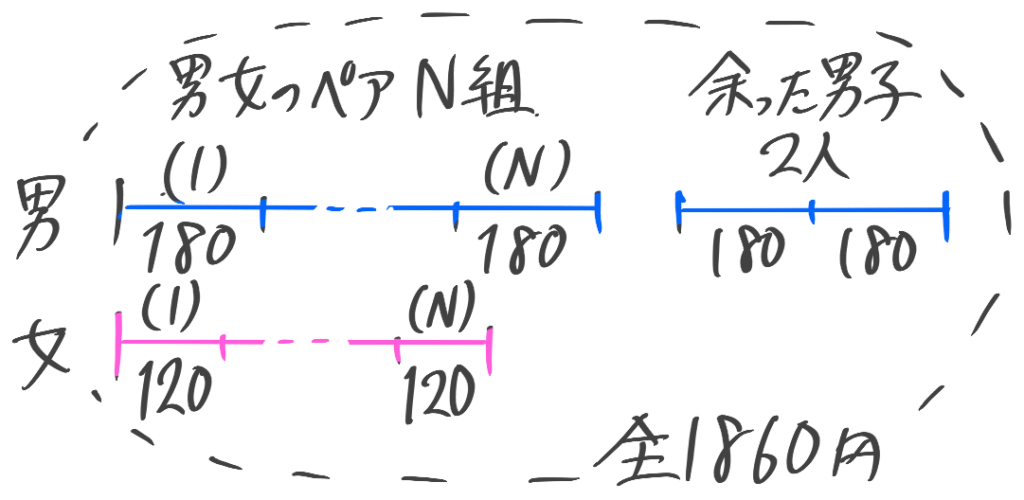
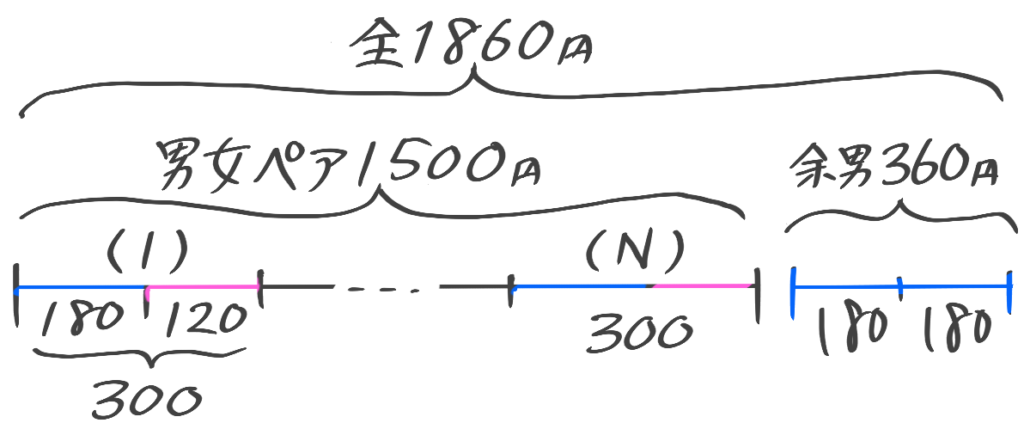
男女のグループを親水公園に連れていき男女ペア300円で乗るボート代として男子には180円ずつ女子には120円ずつ合計1860円を渡したところ、余ってしまった男子達が合わせて360円を返してきた。このグループの男女の人数はそれぞれ何人か。
余った男子は360÷180=2人で、残りの男女は余らずペアを組むので同数と分かる
ここで、180+120=300円を区切りにして男女のペアを1つの線分図にする
ボートに乗るのに使われた金額は1860-360=1500円なので、ボートに乗ったペアの数N=1500÷300=5組。
男子はペアを組めた5人+余った2人=7人。女子は全員ペアを組めた5人と分かります
考えてみたら…余った男子2人でボートに乗れば良かったのにｗ
ペアの差集め算
「ペアの線分図」を利用して差集め算を解く
(問題は省略します。予習シリーズ本体を参照して下さい)
計画Aでは和室と洋室のペアN組に3+2=5人ずつと多い洋室4部屋に2人ずつ生徒を入れ、計画Bではペアに8人ずつと洋室に3人ずつ生徒を入れる。
この問題では計画Bと生徒の人数が同じだから線分は2本で良いので差集め算にしている
(N)の右端の区切りの幅は(2+2+2+2)+40-(3+3+3+3)=36人で、1ペアの差(3)x(N)=36よりN=12組
和室の部屋数(=ペア数=N)=１２部屋、洋室(N+4)=16部屋、人数は8×12+(3+3+3+3)=108人(計画Bより)と分かります
ペアの過不足算
「ペアの線分図」を過不足に利用する
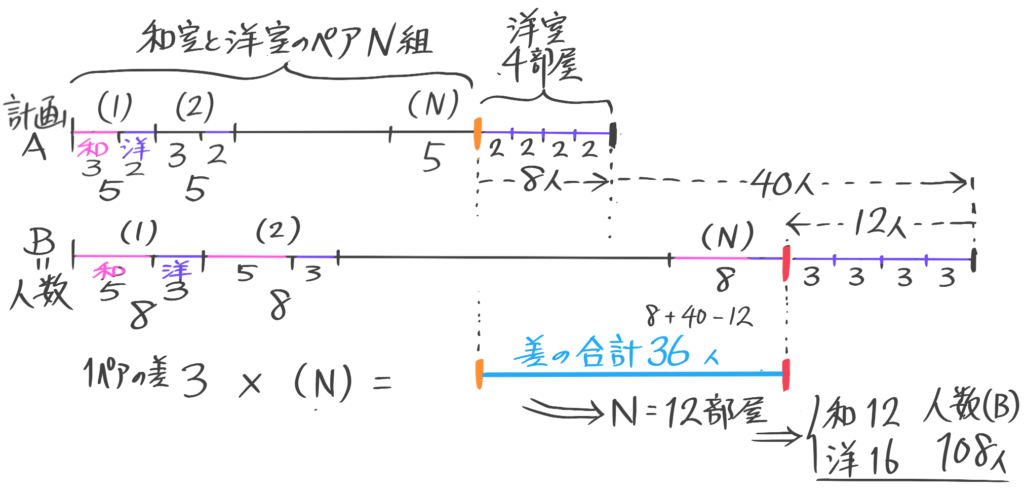
用意したアメを、男子に3個ずつ女子に4個ずつ配ると8個余り、男子に5個ずつ女子に3個ずつ配ると7個足りない。男子が女子より3人多いとき、男女の人数とアメの個数を求めよ
計画Aでは男女のペアに7個ずつと余った男子3人に3個ずつ配り、計画Bではペアに8個ずつと余った男子3人に5個ずつ配る、の間に実際の個数を入れた線分図を書く
ペアをN組として(N)の右端の間=差の合計を出すと、(3+3+3)+8+7-(5+5+5)=24-25=9で、1ペアの差(1)x(N)=9よりN=9組
女子の人数(=ペア数=N)=9人、男子(N+3)=12人、アメの個数は7×9+(3+3+3)+8=80個(計画Aより)と分かります
ご案内
プリント販売(予定)
この記事で扱った基本問題・練習問題の図解プリントを記事公開期間のみの特別価格で販売しています。「教材販売所」の「ヨリシス」を御覧ください。
オンライン授業
ほぼ毎週「予習シリーズ5年」のカリキュラムに沿ったオンラインのスポット授業の生徒さんを募集しています。
無料体験は実施しませんが、初めての方は「ネタ割引」をご使用いただくと野口英世1枚程度で受講が可能です。
1回だけ短時間でも受講可能です。2回目の方は「クーポン」で安く受講が可能です
詳しくは「『そうちゃ式 家庭教師』オンライン授業」を御覧ください
終わりに
爽茶この記事を活用して成績アップを図り、志望校合格へ一歩でも近づくことを祈ります。
焦らず頑張って下さい。応援しています！
