現在、本シリーズの構成を再検討中です
「予習シリーズ」を使っている小5の中学受験生の方へ
この記事では東大卒講師歴20年超の図解講師「そうちゃ」が予習シリーズ5年(上)の第8回「多角形の回転と転がり」を分かりやすく図解します
テキストの分からない問題の図解を「テキスト問題へのリンク」からジャンプして見るのも良し、初めから読んで基礎からステップアップしながらじっくり理解するのも良し、自由に使って実力アップに役立てて下さい!
この記事の完成予定:2023.4.17(月)未明
はじめに(ヨリシスについて)
ヨリシス by そうちゃ式
講師歴25年の図解講師「そうちゃ」が、予習シリーズ(が理解させようとしている学習体系)をスルッと理解できる「ヨリシス (Yo-Resys) by そうちゃ式」を始めます♪
予習シリーズベースで学習している小学5年生で「算数が難しい!」テキストが良くわからない…」と悩んでいる方へそれ、当然の悩みです。予習シリーズは分かりやすいテキストなのですが、4年の途中からだんだん難しくなり5年になると4年内容が前提となるので、1回分の内容は4年の最初と比べると3倍くらい!(マジで)
本来「4年内容の復習→5年内容の導入→定理公式の使い方→例題→標準問題→応用問題」という順番で学習するのが望ましいのに、授業がいきなり例題や標準問題からはじまってしまうと算数が苦手な生徒さんは「ぜんぜん分からない!」となってしまいます(涙)
もちろん、予習シリーズには「復習パート」があるのですが、その量が十分でなく、また例題なしの「いきなり標準問題」や標準問題なしの「いきなり応用問題」もあって、算数が苦手な生徒さんが「予習シリーズ」本体を十分に時間をとって予習しても完全に理解するのは難しいです。
じゃあどうすればいいの…と思ったあなた、お任せ下さい
「ヨリシス」について
「ヨリシス by そうちゃ式」は、算数が苦手な人でも理解しやすいように「予習シリーズ」の中身を並べ替えて(再体系化=リシス)そうちゃの図解を加え、さらに例題・問題の前後や途中に前提となる事柄や4年の復習を「補完例題」「補完問題」として追加したものです
算数が苦手な人でも、つまづいた例題・基本問題・練習問題の前にある「補完問題」を学習すれば、つまづきが解消して練習問題も解けるようになるでしょう。
「ヨリシス」の見方
例題,基本問題,練習問題
→「予習シリーズ」掲載の問題
番号に「’」がついているもの(ダッシュ版)は改題/自作バージョン
ダッシュ版には問題とそうちゃ式の図解がついていますが、ダッシュなしの原本版は著作権保護のため問題文は非掲載で図解のみです。
(例題はできるだけダッシュ版にして問題を掲載しています)
補完例題,補完問題→予習シリーズの例題や問題だけでは理解が難しい場合に、前提事項を基本解法を補うために追加したものです。
分からない問題の前に「補完」がある場合は、まずそちらを読むと良いでしょう♪
学習ガイド
テキストの補習に
各回のはじめに例題(類題)・基本問題・練習問題へのリンクである「問題目次」があります。
テキストを学習していて分からない例題・基本問題・練習問題がはっきりしている場合は、各回最初にある「問題目次」からそうちゃ式の「図解」へとジャンプして下さい
算数が苦手でない人は図解を見て理解できたら、ノートまたは「そうちゃ式ワーク(予リシス)」で自分でも書けるか試せば良いでしょう。
算数が苦手な人は、いきなり図解を見るよりは、その前にある「補完問題」を十分に理解(復習)して、それから図解を学習しましょう。「補完問題」も分からない場合は「そうちゃ式1号館/2号館」の該当記事へジャンプして学習して下さい。
テキストの予習に
算数が苦手な生徒さんは4年の範囲を完全に忘れていることが珍しくありません。授業の前に「ヨリシス by そうちゃ式」で各例題の前にある「補完問題」を解けるようにしておくと4年範囲が復習できて授業が分かりやすくなるでしょう。
テキストの代わりに
塾なしで予習シリーズをベースに学習していて、算数が苦手な人は予習シリーズの代わりに「ヨリシス by そうちゃ式」で学習しても良いでしょう
また講習期間などにテキストを予習・復習したい人も予習シリーズ本体よりも「ヨリシス by そうちゃ式」のほうが学習しやすいと思います。
「ヨリシス」総目次(リンク)
4(上)
4(下)
5(上)
1「約数と倍数」/2「面積の求め方」/3「割合」/4「差集め算(&過不足算)」/5「総合」
6「濃度」/7「売買」/8「多角形の回転/転がり」/9「円の回転/転がり」/10「総合」
11「並べ方」/12「組み合わせ方」/13「速さとグラフ」/14「水量変化」/15「総合」
16「旅人算とグラフ」/17「色々な旅人算」/18「数列と数表」/19「点の移動」/20「総合」
5(下)
テキスト問題へのリンク(未整備)
解き方・解説がよく分からない問題の解説を見たい人はこちらから図解へジャンプして下さい。算数が苦手な人/解説がよく分からない人は、リンク先から少し上にある前提になる問題を見ると理解しやすいでしょう♪
(本回)
◆例題[1(1)/(2)/(3)//2(1)/(2)/(3)//3(1)/(2)
4//5(1)/(2)//6(1)/(2)//7]
◆基本問題[1(1)/(2)/(3)/(4)/(5)/(6)/(7)/(8)/(9)
2(1)/(2)//3(1)/(2)//4//5//6]
◆練習問題[1(1)/(2)//2//3//4(1)/(2)/(3)//5//6]
==================
(総合回:●回)
◆基本問題[1(1)/(2)/(3)/(4)/(5)/(6)/(7)/(8)/(9)/(10)
2//3//4//5//6]
◆練習問題[1//2(1)/(2)//3//4]
今回の学び方
この章では「点」「線」「(平)面」の回転移動から転がり移動までが一気に出てくるので、スモールステップに分解して学びやすくしました。また考え方が分かっても実際に図を書くのが難しい(特に円と弧)ので、書き方のコツを理解して練習してもらうことに重点をおいて再体系化(リシス)をしました。
記事を通して読みながら図を真似して書いてみれば、予習シリーズの原作者が伝えたい内容を体系的に理解する「体験」ができます。
なお「予習シリーズ」に限定せず「そうちゃ式」の体系で最初から学びたい人は関連記事「●●●」を見て下さい
現在の作業状況:体系配置終了→問題図解作成中(~/17)
多角形の回転移動
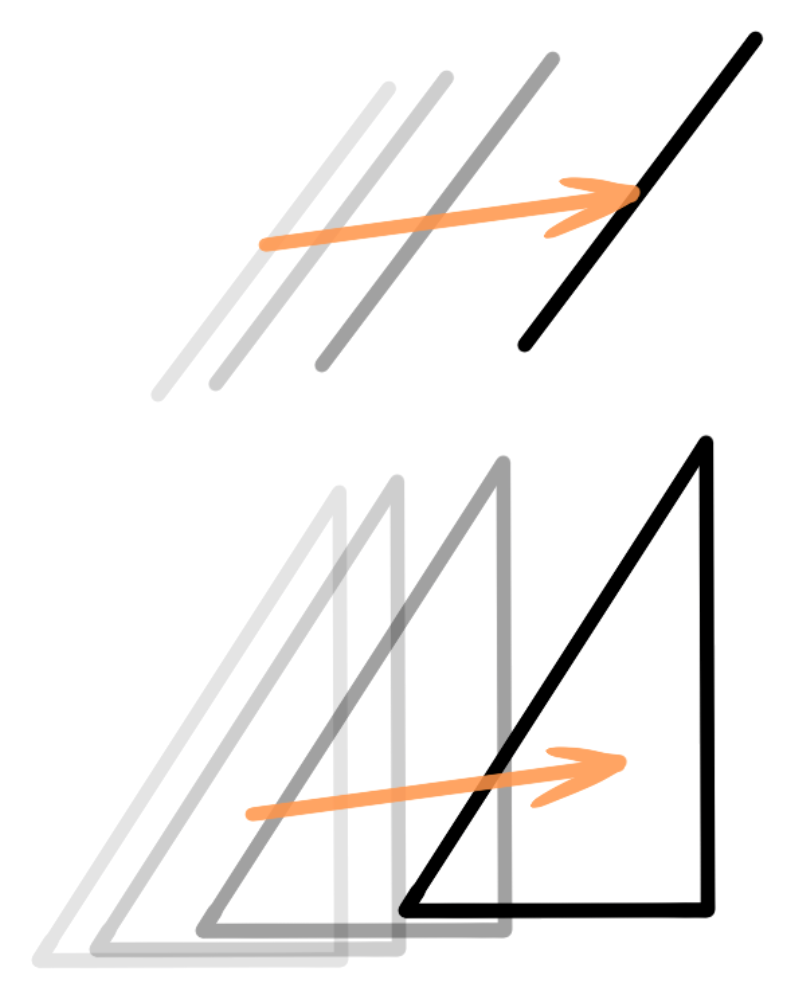
平行移動と回転移動
平行移動は向きも形も変えずに位置だけを移動する。回転移動は形は変わらないが向きが変わる。
回転移動には回転の中心=回転で動かない点(動かす図形の上に無いことも多い)がある
円の描写練習
回転移動の問題は解くときはもちろん、「円」や「おうぎ形」を作図する問題がでるので上手に描けるように練習
[補完例題0]
(1)方眼紙を使った円の書き方
(2)方眼紙を使った45°弧の書き方
(3)方眼紙を使った60°弧の書き方
点の回転移動
[補完例題2-1(1)]方眼上の点の回転移動と軌跡の長さ
(ア)360°回転
円周になる
(イ)未満回転
おうぎ形の弧になる
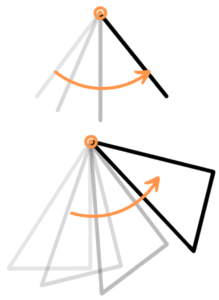
線の回転移動
線が回転すると、動いた跡(軌跡)が平面を作る。軌跡の面積が問題になる
(2種類の図)
まず、中心の位置によって分けて考えてみる
中心が線の上にある場合
[補完例題2-1(2)]方眼上の線の回転移動と軌跡の面積
未満回転→おうぎ形になる
[基本問題1(4)]
補完例題↑を参照
中心が線の上にない場合(A)
[補完例題2-1(3)]
(ア)方眼上の線の360°回転移動と軌跡の面積
(イ)360°未満回転
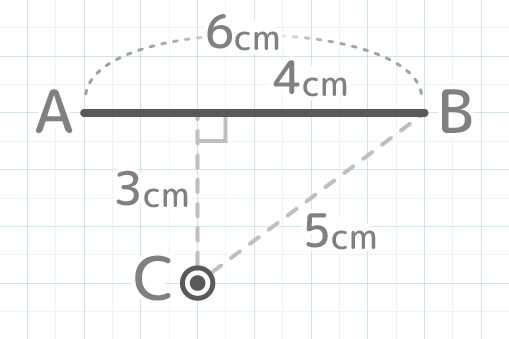
複雑な形に見えるが、遠い点を中心と結んでおうぎ形を作ってPをQに移すと、半径 のおうぎ形と半径 のおうぎ形に囲まれた範囲「バームクーヘン」になると分かる
「回転移動の軌跡の問題はバームクーヘンになる」と考えて大丈夫
結局、中心の位置に関わらず、線の回転移動の軌跡は「中心から一番近い線上の点」の軌跡と「〃一番遠い線上の点」の軌跡に囲まれた範囲になる。
→回転の中心から一番遠い点と一番近い点を
回転させて、囲まれた部分が軌跡になる。
[基本問題4]
↑参照。半径10cmと8cm、中心角90°のバームクーヘンになる
中心が線の上にない場合(B)
(最近点が両端でない場合)
[例題3′]辺の回転移動
webの問題そのもの
「中心から一番近い線上の点」Dの軌跡と「〃一番遠い線上の点」Cの軌跡に囲まれた範囲になる
[練習問題2]
(1)未満回転→外径25cm内径20cm中心角64°のバームクーヘンになる
(2)360°回転→最近点Dと最遠点Cの外径20cm内径12cmのドーナツになる
折れ線の回転移動
例題なしだが、入試でも頻出
[補完例題2-1(3)]線上に中心
(おうぎ形+三角形)-三角形=おうぎ形
このように、結局おうぎ形になる
[練習問題1′]
補完例題2-1(3)↑参照
(中心A半径6cm中心核30°のおうぎ形+三角形AB’C’)-三角形ABC=おうぎ形
三角形の回転移動
特徴
形が変わらない~合同な図形が出来る
→同じ長さ・角度に同じ印をつけること!
[例題1′]二等辺三角形の回転移動と角度
[基本問題1(1)]正三角形の~
例題1’↑を参照
[総合(10回)基本問題6]
例題1’↑を参照
[基本問題1(2)]正方形の
例題1’↑を参照
[基本問題2]凡三角形の~
例題1’↑を参照
頂点・辺の軌跡
「点の回転移動」「辺の回転移動」と同様に考える
[例題2′(1)(2)(3)]三角形の頂点の回転移動の軌跡
2辺の軌跡
「折れ線の回転移動」と同じ
[例題2′(A)]三角形の二辺の回転移動の軌跡
面全体の軌跡
[例題2′(B)]三角形全体の回転移動の軌跡
[基本問題1(5)’]
°のおうぎ形と三角形ABCを合わせた形になる
[総合(10回)基本問題7]
例題2′(B)↑を参照
四角形の回転移動
[総合(10回)練習問題1′]
回転移動は以上です♪
多角形の転がり移動
転がり移動の様子
こんな移動です。
回っているので回転移動に似ていますが、回転移動は回転の中心がきまっていたのに対して、この動きは回転の中心が変わっています。このように「中心が変化する連続した回転移動」が転がり移動です
(正)(長)方形の転がり
転がりの様子
[例題4′(0)]
頂点の決め方
[基本問題1(3)]
例題4′(0)↑参照
頂点の軌跡など
[例題4′(1)(2)]
方形の軌跡
[例題4′(A)]
[練習問題4]
例題4′(A)↑を参照
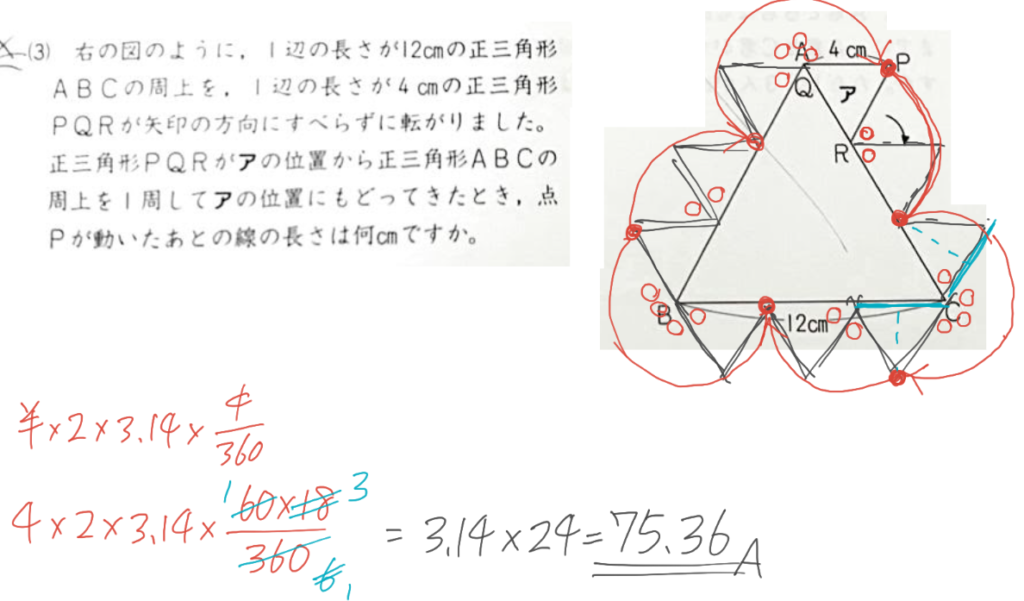
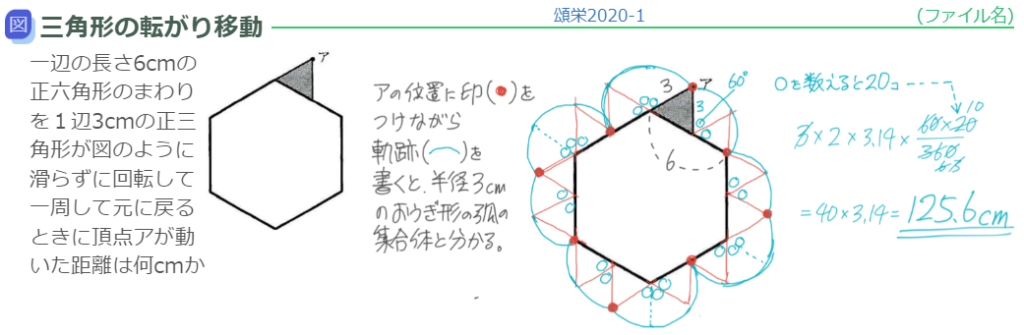
正三角形
直線上を転がる
[基本問題3′]
(1)直線状を転がる正三角形の頂点の位置を把握する練習
(2)ある頂点の軌跡の長さ
(3)全体の軌跡面積
[総合(10回)基本問題8]
基本問題3’↑を参照
折れ線上を転がる
[例題5′]
[総合(10回)練習問題5]
例題5’↑を参照
方形の内外を転がる
[練習問題3′]
その他の図形
(問題の文章をここに入れる)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題の文章をここに入れる)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題の文章をここに入れる)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題の文章をここに入れる)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題の文章をここに入れる)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題の文章をここに入れる)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題の文章をここに入れる)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題の文章をここに入れる)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題の文章をここに入れる)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(1) (問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(2) (問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
((問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
– – – – – – – – – – – – – – – – – – –
(問題文省略。テキストを見て下さい)
(解答をここに入れる)
ご案内
プリント販売(予定)
この記事で扱った基本問題・練習問題の図解プリントを記事公開期間のみの特別価格で販売しています。「教材販売所」の「ヨリシス」を御覧ください。
オンライン授業
ほぼ毎週「予習シリーズ5年」のカリキュラムに沿ったオンラインのスポット授業の生徒さんを募集しています。
無料体験は実施しませんが、初めての方は「ネタ割引」をご使用いただくと野口英世1枚程度で受講が可能です。
1回だけ短時間でも受講可能です。2回目の方は「クーポン」で安く受講が可能です
詳しくは「『そうちゃ式 家庭教師』オンライン授業」を御覧ください
終わりに
 爽茶
爽茶この記事を活用して成績アップを図り、志望校合格へ一歩でも近づくことを祈ります。
焦らず頑張って下さい。応援しています!